Câu hỏi:
2 năm trước
Cho hai điện tích điểm \({q_1} = {6.10^{ - 7}}C;{q_2} = - {8.10^{ - 7}}C\) đặt tại hai điểm A và B trong không khí cách nhau \(5cm.\) Xác định véc tơ cường độ điện trường tổng hợp tại M do \({q_1}\) và \({q_2}\) gây ra tại M biết \(MA = 3cm, MB = 8cm.\)
Trả lời bởi giáo viên
Đáp án đúng: b
+ Cường độ điện trường do điện tích \({q_1}\) gây ra tại M:
\({E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{M^2}}} = {9.10^9}\dfrac{{\left| {{{6.10}^{ - 7}}} \right|}}{{0,{{03}^2}}} = {60.10^5}V/m\)
+ Cường độ điện trường do điện tích \({q_2}\) gây ra tại M:
\({E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{B{M^2}}} = {9.10^9}\dfrac{{\left| { - {{8.10}^{ - 7}}} \right|}}{{0,{{08}^2}}} = 11,{25.10^5}V/m\)
Cường độ điện trường tổng hợp tại M: \(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} {\rm{ }}\)
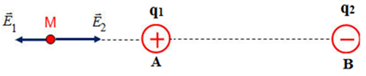
Từ hình vẽ ta có: \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \Rightarrow E = \left| {{E_1} - {E_2}} \right|\)
\( \Rightarrow E = \left| {{{60.10}^5} - 11,{{25.10}^5}} \right| = 48,{75.10^5}V/m\)
Hướng dẫn giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường: \(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
