Bài tập Công của lực điện - Hiệu điện thế

Gọi  ${A_1}$ - là công của lực điện trường khi dịch chuyển electron quãng đường $0,6cm$

${A_2}$ - là công của lực điện trường khi dịch chuyển electron quãng đường \({s_2} = 0,6 + 0,4 = 1cm\)

Ta có:

$\begin{array}{*{20}{l}}{{A_1} = {\rm{ }}9,{{6.10}^{ - 18}}J,{\rm{ }}{s_1} = {\rm{ }}0,6cm,{\rm{ }}e{\rm{ }} = {\rm{ }} - 1,{{6.10}^{ - 19}}C,{\rm{ }}{m_e} = {\rm{ }}9,{{1.10}^{ - 31}}kg}\\{{s_2} = {\rm{ }}0,4{\rm{ }} + {\rm{ }}0,6{\rm{ }} = {\rm{ }}1cm,{\rm{ }}{v_0} = {\rm{ }}0}\end{array}$

Lực điện sinh công dương => electron chuyển động ngược chiều điện trường \(\alpha = {\text{ }}{180^0}\)

${A_1} = qE{s_1}cos\alpha  \to E = \dfrac{{{A_1}}}{{e.{s_1}{\rm{cos18}}{{\rm{0}}^0}}} = \dfrac{{9,{{6.10}^{ - 18}}}}{{ - 1,{{6.10}^{ - 19}}.0,006.{\rm{cos18}}{{\rm{0}}^0}}} = {10^4}V/m$

Mặt khác, ta có: ${A_{1}}{\text{ = }}{W_{{d_1}}} - {W_{{d_0}}} = \dfrac{1}{2}m{v_1}^2 - \dfrac{1}{2}m{v_0}^2 = \dfrac{1}{2}m{v_1}^2$

\(\begin{gathered}  {A_2} = qE{s_2}cos\alpha  = 1,{6.10^{ - 17}}J \hfill \\  {A_{2}}{\text{ = }}{W_{{d_2}}} - {W_{{d_0}}} = \frac{1}{2}mv_2^2 -\frac{1}{2}mv_0^2=\frac{1}{2}mv_2^2 \hfill \\   \Rightarrow \frac{1}{2}mv_2^2 = {A_{2}} \hfill \\   \Rightarrow {v_2} = \sqrt {\frac{{2{A_2}}}{m}}  = \sqrt {\frac{{2.1,{{6.10}^{ - 17}}}}{{9,{{1.10}^{ -31}}}}}  = 5,{9.10^6}m/s \hfill \\\end{gathered} \)

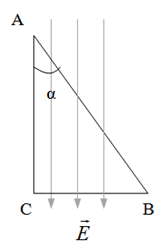
Hiệu điện thế U_AB:

\({U_{AB}} = E.{d_{AB}} = E.ABc{\rm{os}}\alpha  = E.AB\frac{{AC}}{{AB}} = E.AC = 5000.0,04 = 200V\)

Áp dụng định lí động năng ta có:

\(\begin{gathered}\Delta {\text{W}} = {W_{{_2}}} - {W_{{_1}}} = A = 250{\text{e}}V = 250.1,{6.10^{ - 19}} = {4.10^{ - 17}}J \hfill \\{U_{MN}} = \frac{A}{q} = \frac{A}{e} = \frac{{{{4.10}^{ - 17}}}}{{ - 1,{{6.10}^{ - 19}}}} =  - 250V \hfill \\\end{gathered} \)

Mốc điện thế tại $A{\rm{ }} => {\rm{ }}{V_A} = {\rm{ }}0$

\(\begin{array}{*{20}{l}}\begin{array}{l}{U_{AB}} = {\rm{ }}{E_1}.{d_1} = {\rm{ }}{V_A} - {\rm{ }}{V_B}\\ \Rightarrow {V_B} = {\rm{ }}{{\rm{V}}_A} - {E_1}.{d_1} = 0 - {4.10^4}.0,05{\rm{ }} =  - 2000V\end{array}\\\begin{array}{l}{U_{CB}} = {\rm{ }}{E_2}.{d_2} = {\rm{ }}{V_C} - {\rm{ }}{V_B}\\ \Rightarrow {V_C} = {E_2}.{d_2} + {V_B} = {5.10^4}.0,08{\rm{ }} - 2000 = 2000V\end{array}\end{array}\)

Ta có, khi electron di chuyển từ A đến B thì chịu tác dụng của ngoại lực là lực điện trường nên theo định lí động năng, ta có:

\(\begin{array}{l}{{\rm{W}}_{{d_B}}} - {{\rm{W}}_{{d_A}}} = {A_{ngoailuc}} \leftrightarrow 0 - \frac{1}{2}mv_A^2 = qE{{\rm{d}}_{AB}}\\ \to E = \frac{{mv_A^2}}{{2\left| {q{{\rm{d}}_{AB}}} \right|}} = \frac{{9,{{1.10}^{ - 31}}.{{({{5.10}^6})}^2}}}{{2\left| {{\rm{ - 1,6}}{\rm{.1}}{{\rm{0}}^{ - 19}}{\rm{.0,1}}} \right|}} = 710,94V/m\end{array}\)

Ta có, các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \) , lực điện \(\overrightarrow F \)

+ Điều kiện cân bằng của quả cầu: \(\overrightarrow F  + \overrightarrow P  = 0 \to F = P \leftrightarrow qE = mg\)

Mặt khác, \(U = E.d = \frac{{mg}}{q}d = \frac{{3,{{06.10}^{ - 15}}.10}}{{4,{{8.10}^{ - 18}}}}.0,02 = 127,5V\)

Các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \) , lực điện \(\overrightarrow F \)

+ Điều kiện cân bằng của quả cầu: \(\overrightarrow F  + \overrightarrow P  = 0 \to F = P \leftrightarrow qE = mg \to q = \frac{{mg}}{E}\)

Mặt khác: \(E = \frac{U}{d} \to q = \frac{{mg}}{{\frac{U}{d}}} = \frac{{mgd}}{U}\)

Áp dụng cho lúc đầu và lúc sau, ta có: \(\left\{ \begin{array}{l}{q_1} = \frac{{mg{\rm{d}}}}{U}\\{q_2} = \frac{{mg{\rm{d}}}}{{U + \Delta U}}\end{array} \right.\)

\( \to \Delta q = {q_1} - {q_2} = mg{\rm{d}}\left( {\frac{1}{U} - \frac{1}{{U + \Delta U}}} \right) = {10^{ - 11}}{\rm{.1}}{{\rm{0}}^{ - 3}}{\rm{.10}}{\rm{.0,005}}{\rm{.}}\left( {\frac{1}{{306,3}} - \frac{1}{{306,3 + 34}}} \right) = 1,{63.10^{ - 19}}C\)

Các lực tác dụng lên hạt bụi gồm: Trọng lực \(\overrightarrow P \) , lực điện \(\overrightarrow F \)

+ Điều kiện cân bằng của hạt bụi:

 \(\overrightarrow F  + \overrightarrow P  = 0 \to F = P \leftrightarrow qE = mg \to q = \dfrac{{mg}}{E}\)

Mặt khác: \(E = \dfrac{U}{d} \to q = \dfrac{{mg}}{{\dfrac{U}{d}}} = \dfrac{{mgd}}{U}\) (1)

Sau khi giảm hiệu điện thế giữa hai bản tụ thì hạt bụi chuyển động biến đổi đều nên theo định luật II-Newtơn ta có:  

\(\overrightarrow {F'}  + \overrightarrow P  = m\overrightarrow a \) (*)

Chọn chiều dương là chiều chuyển động (hướng xuống), chiếu (*) ta được:

\(P - F' = ma \leftrightarrow mg - qE' = ma \leftrightarrow mg - q\dfrac{{U - \Delta U}}{d} = ma\) (2)

Thế (1) vào (2), ta được: \(a = g - g\left( {\dfrac{{U - \Delta U}}{U}} \right) = \dfrac{{49}}{{25}}m/{s^2}\)

Mặt khác, ta có: \(s = d = \dfrac{1}{2}a{t^2} \to t = \sqrt {\dfrac{{2{\rm{d}}}}{a}}  = 0,09{\rm{s}}\)

Khi điện tích q di chuyển từ vô cùng về M thì nó chịu tác dụng của lực do tay tác dụng và lực điện (do điện trường của quả cầu gây ra)

Gọi A - công của lực điện trường của quả cầu sinh ra khi di chuyển q

Ta có: A = -A’ = -5.10^-7J

Mặt khác, ta có: \(A = q({V_\infty } - {V_M}) =  - q{V_M}\)

=> điện thế do quả cầu sinh ra là \({V_M} = \frac{A}{{ - q}} = \frac{{ - {{5.10}^{ - 7}}}}{{ - {{10}^{ - 9}}}} = 500V\)

Gọi Q là điện tích quả cầu, điện thế tại M:

\({V_M} = k\frac{Q}{{{r_M}}} \to Q = \frac{{{V_M}{r_M}}}{k} = \frac{{500.0,24}}{{{{9.10}^9}}} = \frac{{40}}{3}{.10^{ - 9}}C\)

Vậy điện thế do quả cầu gây ra tại bề mặt quả cầu là:

\({V_0} = k\frac{Q}{{{r_0}}} = {9.10^9}\frac{{\frac{{40}}{3}{{.10}^{ - 9}}}}{{0,04}} = 3000V\)

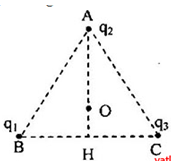
- Điện thế tại O:

\({V_0} = {V_{10}} + {V_{20}} + {V_{30}} = k\frac{{{q_1}}}{{OA}} + k\frac{{{q_2}}}{{OB}} + \frac{{{q_3}}}{{OC}}\)

Ta có, tam giác ABC đều

\( =  > OA = OB = OC = \frac{2}{3}\frac{{10\sqrt 3 }}{2} = \frac{{10}}{{\sqrt 3 }}cm = \frac{{0,1}}{{\sqrt 3 }}m\)

\( \to {V_0} = \frac{k}{{OA}}({q_1} + {q_2} + {q_3}) = \frac{{{{9.10}^9}}}{{\frac{{0,1}}{{\sqrt 3 }}}}({15.10^{ - 9}} - {12.10^{ - 9}} + {7.10^{ - 9}}) = 1558,8(V)\)

- Điện thế tại H do các điện tích điểm gây ra là:

\({V_H} = {V_{1H}} + {V_{2H}} + {V_{3H}} = k\frac{{{q_1}}}{{AH}} + k\frac{{{q_2}}}{{BH}} + \frac{{{q_3}}}{{CH}}\)

Ta có: \(\left\{ \begin{array}{l}AH = \frac{{10\sqrt 3 }}{2}cm = 0,05\sqrt 3 m\\HB = HC = 5cm = 0,05m\end{array} \right.\)

\({V_H} = {9.10^9}(\frac{{{{15.10}^{ - 9}}}}{{0,05\sqrt 3 }} + \frac{{ - {{12.10}^{ - 9}}}}{{0,05}} + \frac{{{{7.10}^{ - 9}}}}{{0,05}}) = 658,8V\)

Để hai hạt proton lại gần nhau hơn, ta có thể để một hạt proton đứng yên, còn proton kia di chuyển từ A đến B.

Gọi O là vị trí của proton đứng yên, A là vị trí ban đầu của proton cần di chuyển, B là vị trí lúc sau khi di chuyển của proton đó.

Ta có: $OA = 1m;OB = 0,5m$

Điện thế do proton đứng yên tại O gây ra tại A và B là:

       + Tại A: \({V_A} = k\frac{q}{{{r_A}}} = {9.10^9}\frac{{1,{{6.10}^{ - 19}}}}{1} = 14,{4.10^{ - 10}}V\)

       + Tại B: \({V_B} = k\frac{q}{{{r_B}}} = {9.10^9}\frac{{1,{{6.10}^{ - 19}}}}{{0,5}} = 28,{8.10^{ - 10}}V\)

Công của lực điện trường khi proton thứ hai di chuyển từ A đến B là:

$A = q({V_A} - {V_B}) = {1,6.10^{ - 19}}({14,4.10^{ - 10}} - {28,8.10^{ - 10}}) = - {23,04.10^{ - 29}}J$

Công của điện trường là công cản => Công cần thiết để di chuyển proton từ A đến B là:

A’ = - A = 23,04.10^-29J

Do q₁.q₂ > 0 nên vị trí điểm M có cường độ điện trường tổng hợp bằng 0 nằm trong khoảng giữa q₁ và q₂.

Gọi x là khoảng cách từ vị trí điểm M đến điện tích q₁

Ta có, tại M cường độ điện trường tổng hợp bằng 0, nên ta có:

\(\begin{array}{l}\overrightarrow {{E_1}}  + \overrightarrow {{E_2}}  = 0 \to {E_1} = {E_2} \leftrightarrow k\frac{{{q_1}}}{{{x^2}}} = k\frac{{{q_2}}}{{{{(a - x)}^2}}}\\ \leftrightarrow a - x = 2{\rm{x}} \to x = \frac{a}{3} = 3cm = 0,03m\end{array}\)

Điện thế tại M:

\(\begin{array}{l}{V_M} = {V_{1M}} + {V_{2M}} = k\frac{{{q_1}}}{x} + k\frac{{{q_2}}}{{a - x}}\\ = {9.10^9}(\frac{{{{10}^{ - 9}}}}{{0,03}} + \frac{{{{4.10}^{ - 9}}}}{{0,09 - 0,03}}) = 900V\end{array}\)

Thế năng tĩnh điện của hai điện tích: \({{\rm{W}}_t} = k\frac{{{q_1}{q_2}}}{r} = {9.10^9}\frac{{{{10}^{ - 8}}.( - {{2.10}^{ - 8}})}}{{0,1}} =  - 1,{8.10^{ - 5}}J\)

Ta có:

+ Lúc đầu năng lượng của hệ là thế năng tương tác tĩnh điện: \({{\rm{W}}_1} = k\dfrac{{{e^2}}}{r}\)

+ Khi nó vừa thoát ra thì có vận tốc v, lúc này nó không chịu lực hút của proton nên lúc này hệ không còn thế năng tương tác mà chỉ có động năng: \({{\rm{W}}_2} = \dfrac{1}{2}m{v^2}\)

Áp dụng định luật bảo toàn năng lượng, ta có:

\({{\rm{W}}_1} = {{\rm{W}}_2}\\ \leftrightarrow k\dfrac{{{e^2}}}{r} = \dfrac{1}{2}m{v_0}^2 \\\to {v_0} = \sqrt {\dfrac{{2{{\rm{e}}^2}}}{{m{\rm{r}}}}}  = 3,{2.10^6}m/s\)

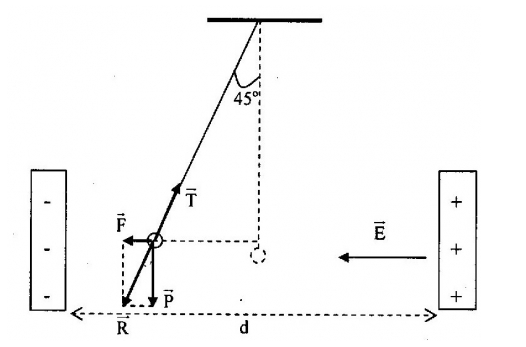
Ta có, các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \) , lực điện \(\overrightarrow F \), lực căng dây \(\overrightarrow T \)

+ Điều kiện cân bằng của quả cầu: \(\overrightarrow T  + \overrightarrow F  + \overrightarrow P  = 0 \to \overrightarrow T  + \overrightarrow R  = 0\)

=> \(\overrightarrow R \)có phương sợi dây

Ta có:

\(\begin{array}{l}\tan {45^0} = \frac{F}{P} \to F = P \leftrightarrow qE = mg \leftrightarrow q\frac{U}{d} = mg\\ \to U = \frac{{mg{\rm{d}}}}{q} = 200V\end{array}\)

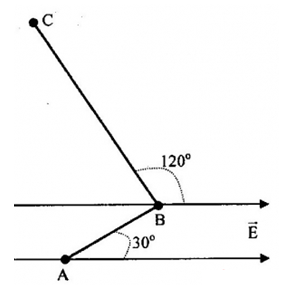
Từ hình, ta có:

\(\left\{ \begin{array}{l}{d_{AB}} = ABc{\rm{os3}}{{\rm{0}}^0} = 20.\frac{{\sqrt 3 }}{2} = 10\sqrt 3 cm\\{d_{BC}} = BCc{\rm{os12}}{{\rm{0}}^0} = 40.\left( { - \frac{1}{2}} \right) =  - 20cm\end{array} \right.\)

Công của lực điện khi làm điện tích q di chuyển theo đường gấp khúc ABC là:

\(\begin{array}{l}A = {A_{AB}} + {A_{BC}} = qE\left( {{d_{AB}} + {d_{BC}}} \right)\\ = {4.10^{ - 8}}.100(0,1\sqrt 3  + ( - 0,2))\\ =  - 1,{07.10^{ - 7}}J\end{array}\)

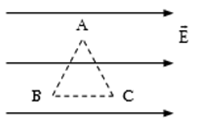
Công của lực điện trường khi q di chuyển trên cạnh AB là:

\({A_{AB}}\; = q.E.AB.cos{120^0} = {10^{ - 8}}.300.0,1.\left( { - 0,5} \right){\rm{ }} =  - 1,{5.10^{ - 7}}\;J\)

Công của lực điện trường khi q di chuyển trên cạnh BC là:

\({A_{BC}}\; = q.E.BC = {10^{ - 8}}.300.0,1 = {3.10^{ - 7}}\;J\)

Công của lực điện trường khi q di chuyển trên cạnh AC là:

\({A_{AC}}\; = q.E.AC.cos60 = {10^{ - 8}}.300.0,1.0,5 = 1,{5.10^{ - 7}}\;J\)

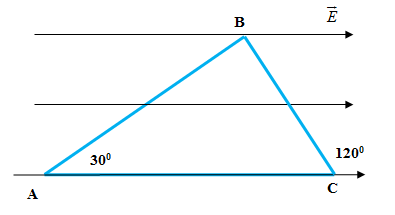
\(\begin{array}{*{20}{l}}{{A_{ABC}}\; = {A_{AB}}\; + {\rm{ }}{A_{BC}}}\\{{A_{AB}}\; = qE{d_1}\; = qE.AB.\cos 30 = {{4.10}^{ - 8}}.100.ABcos30\; = 0,{{7.10}^{ - 6}}J}\\{{A_{BC}}\; = qE{d_2} = qE.BC.\cos {{120}^o} = {{4.10}^{ - 8}}.100.BC.\cos 120\; =  - 0,{{8.10}^{ - 6}}J}\\{ \Rightarrow {A_{ABC}}\; = {A_{AB}}\; + {\rm{ }}{A_{BC}} =  - 0,{{1.10}^{ - 6}}J}\end{array}\)

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{A_{MN}} = qE{d_1}}\\{{A_{NP}} = qE{d_2}}\end{array}} \right.\)

\( \Rightarrow \frac{{{A_{NP}}}}{{{A_{MN}}}} = \frac{{{d_2}}}{{{d_1}}} \Rightarrow {A_{NP}} = {A_{MN}}.\frac{{{d_2}}}{{{d_1}}} = 9,{6.10^{ - 18}}.\frac{{0,4}}{{0,6}} = 6,{4.10^{ - 18}}\,\,\left( J \right)\)

Công của lực điện khi electron di chuyển từ điểm M đến điểm P là:

\({A_{MP}} = {A_{MN}} + {A_{NP}} = (9,6 + 6,4){.10^{ - 18}} = {16.10^{ - 18}}\,\,\left( J \right)\)

Theo định lí động năng ta có:

\(\begin{array}{l}
{A_{MP}} = {{\rm{W}}_{dP}} - {{\rm{W}}_{dM}} \Rightarrow {A_{MP}} = \frac{{mv_P^2}}{2} - \frac{{mv_M^2}}{2} \Rightarrow {A_{MP}} = \frac{{mv_P^2}}{2}\\
\Rightarrow {v_P} = \sqrt {\frac{{2{A_{MP}}}}{m}} = \sqrt {\frac{{{{2.16.10}^{ - 18}}}}{{9,{{1.10}^{ - 31}}}}} = 5,{93.10^6}\,\,\left( {m/s} \right)
\end{array}\)

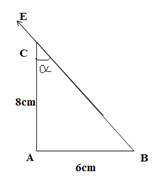
Tam giác ABC vuông tại A có AB = 6cm, AC = 8cm nên BC = 10cm

            U_AC = E.AC.cosα = 3000.0,08.8/10 = 192V