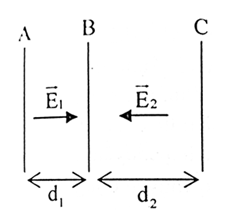
Cho $3$ bản kim loại $A,{\rm{ }}B,{\rm{ }}C$ đặt song song có ${d_1} = {\rm{ }}5cm,{\rm{ }}{d_2} = {\rm{ }}8cm$. Điện trường giữa các bản là điện trường đều, có chiều như hình vẽ với độ lớn ${E_1} = {\rm{ }}{4.10^4}V/m,{\rm{ }}{E_2} = {\rm{ }}{5.10^4}V/m$. Điện thế ${V_B}$ và ${V_C}$ của bản $B$ và $C$ là bao nhiêu? Chọn mốc điện thế tại $A$

Trả lời bởi giáo viên
Mốc điện thế tại $A{\rm{ }} => {\rm{ }}{V_A} = {\rm{ }}0$
\(\begin{array}{*{20}{l}}\begin{array}{l}{U_{AB}} = {\rm{ }}{E_1}.{d_1} = {\rm{ }}{V_A} - {\rm{ }}{V_B}\\ \Rightarrow {V_B} = {\rm{ }}{{\rm{V}}_A} - {E_1}.{d_1} = 0 - {4.10^4}.0,05{\rm{ }} = - 2000V\end{array}\\\begin{array}{l}{U_{CB}} = {\rm{ }}{E_2}.{d_2} = {\rm{ }}{V_C} - {\rm{ }}{V_B}\\ \Rightarrow {V_C} = {E_2}.{d_2} + {V_B} = {5.10^4}.0,08{\rm{ }} - 2000 = 2000V\end{array}\end{array}\)
Hướng dẫn giải:
Áp dụng biểu thức mối liên hệ giữa cường độ điện trường và hiệu điện thế: \(E = \dfrac{U}{d}\)