1. Đường thẳng vuông góc với mặt phẳng
* Đường thẳng d vuông góc với mặt phẳng (\(\alpha \)). Ký hiệu: \(d \bot (\alpha )\)
* Nếu \(\left\{ \begin{array}{l}d \bot (\alpha )\\a \subset (\alpha )\end{array} \right.\)\( \Rightarrow \) \(d \bot a\)
* Nếu \(\left\{ \begin{array}{l}d \bot a \subset (\alpha )\\d \bot b \subset (\alpha )\\ \text {a và b cắt nhau}\end{array} \right.\)\( \Rightarrow \) \(d \bot (\alpha )\)
* Trong tam giác ABC, nếu \(\left\{ \begin{array}{l}d \bot AC\\d \bot AB\end{array} \right.\)\( \Rightarrow \) \(d \bot BC\)
* Nếu \((\alpha )\) là mặt phẳng trung trực của AB\( \Leftrightarrow \)\(\left\{ \begin{array}{l}(\alpha ) \bot AB\,\text{tại}\,I\\I\,\text{là trung điểm của}\,AB\,\,(\text {tức là}\,IA = IB)\end{array} \right.\)
* Nếu M thuộc mp trung trực của AB thì MA = MB
* Nếu AB, AC, AD cùng vuông góc với đt d thì AB, AC, AD đồng phẳng (phải chung một điểm A)
* Nếu \(\left\{ \begin{array}{l}a//b\\a \bot (\alpha )\end{array} \right.\)\( \Rightarrow \) \(b \bot (\alpha )\)
* Nếu \(\left\{ \begin{array}{l}(\alpha )//(\beta )\\d \bot (\alpha )\end{array} \right.\)\( \Rightarrow \) \(d \bot (\beta )\)
* Nếu \(\left\{ \begin{array}{l}d \bot (\alpha )\\d \bot (\beta )\end{array} \right.\) \( \Rightarrow \)\((\alpha )//(\beta )\)
* Nếu \(\left\{ \begin{array}{l}a \bot (\alpha )\\b \bot (\alpha )\end{array} \right.\)\( \Rightarrow \) \(a//b\)
* Nếu \(AH \bot (\alpha )\) thì + H là hình chiếu vuông góc của A trên \((\alpha )\)
+ OH là hình chiếu vuông góc của AO trên \((\alpha )\)
+ \(\widehat {AOH}\) là góc giữa AO và mp\((\alpha )\)với \({0^0} \le \widehat {AOH} \le {90^0}\)
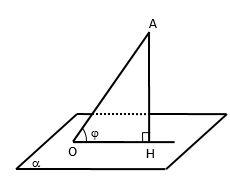
* Định lý ba đường vuông góc
Nếu \(\left\{ \begin{array}{l}b'\,\text{là hình chiếu của}\,b\,\text{trên}\,(\alpha )\\a \bot b\end{array} \right.\)\( \Rightarrow \) \(a \bot b'\)
* Nếu: + O là tâm đường tròn ngoại tiếp \(\Delta \)ABC
+ Đường thẳng d đi qua O và vuông góc với \(\Delta \)ABC
\( \Rightarrow \) d là trục của \(\Delta \)ABC. Khi đó: \(M \in d\)\( \Rightarrow \) MA = MB = MC
* Giao điểm của 3 đường trung trực của \(\Delta \)ABC là tâm đường tròn ngoại tiếp \(\Delta \)ABC
* Nếu \(\Delta \)ABC là tam giác vuông tại A thì tâm đường tròn ngoại tiếp của \(\Delta \)ABC là trung điểm của cạnh huyền BC
* Nếu \(\Delta \)ABC là tam giác đều thì tâm đường tròn ngoại tiếp của \(\Delta \)ABC là giao điểm của 3 đường cao (hoặc 3 đường phân giác, 3 đường trung tuyến, 3 đường trung trực)
* Nếu ABCD là hình vuông (hoặc hình chữ nhật) thì tâm đường tròn ngoại tiếp hình vuông là giao điểm của 2 đường chéo
* Trong tam giác :
+ Giao điểm của 3 đường cao gọi là trực tâm
+ Giao điểm của 3 đường trung tuyến gọi là trọng tâm
2. Hai mặt phẳng vuông góc
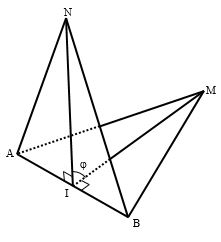
* Góc giữa hai mặt phẳng (ABM) và (ABN) cắt nhau theo giao tuyến AB
Nếu \(\left\{ \begin{array}{l}MI \bot AB\\NI \bot AB\end{array} \right.\) thì \(\widehat {MIN}\)là góc giữa (ABM) và (ABN)
* Diện tích hình chiếu vuông góc của một đa giác :
Nếu S là diện tích của đa giác H nằm trong (\(\alpha \)), S1 là diện tích
của đa giác H1 nằm trong (\(\beta \)), H1 là hình chiếu vuông góc của H
thì \({S_1} = S\cos \varphi \) với \(\varphi \) là góc giữa 2 mp(\(\alpha \)) và (\(\beta \))
* Hai mp(\(\alpha \)) và (\(\beta \)) vuông góc với nhau. Kí hiệu: \((\alpha ) \bot (\beta )\)
* Nếu \(\left\{ \begin{array}{l}d \subset (\alpha )\\d \bot (\beta )\end{array} \right.\)\( \Rightarrow \)\((\alpha ) \bot (\beta )\)
* Hình lăng trụ đứng: là hình lăng trụ có các cạnh bên vuông góc với đáy. Độ dài cạnh bên là chiều cao của lăng trụ đứng. Hai mặt đáy song song, bằng nhau và cùng vuông góc với các cạnh bên. Các mặt bên là những hình chữ nhật
* Hình lăng trụ đứng có đáy là tam giác, tứ giác, ngũ giác, ... gọi là hình lăng trụ đứng tam giác,
hình lăng trụ đứng tứ giác, hình lăng trụ đứng ngũ giác,...
* Hình lăng trụ đều: là hình lăng trụ đứng có đáy là đa giác đều. VD: Hình lăng trụ tam giác đều, hình lăng trụ tứ giác đều
* Hình hộp đứng: là hình lăng trụ đứng có đáy là hình bình hành
* Hình hộp chữ nhật: là hình lăng trụ đứng có đáy là hình chữ nhật
* Hình lập phương: là hình lăng trụ đứng có đáy là hình vuông
* Hình chóp đều: + Đáy là đa giác đều
+ Các mặt bên là những tam giác cân bằng nhau. Các mặt bên tạo với đáy các góc bằng nhau
+ Các cạnh bên bằng nhau và tạo với đáy các góc bằng nhau
+ Chân đường cao trùng với tâm của đáy

