1. Kiến thức cần nhớ
Định nghĩa:
- Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói góc giữa đường thẳng a và mặt phẳng (P) bằng 900.
- Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a′ của nó trên (P) gọi là góc giữa đường thẳng a và mặt phẳng (P).
Kí hiệu:
Nếu a⊥(P) thì ^(a,(P))=900
Nếu a không vuông góc với (P) thì ^(a,(P))=^(a,a′) với a′ là hình chiếu của a trên (P).
Chú ý: 00≤^(a,(P))≤900
2. Bài toán góc giữa đường thẳng và mặt phẳng
Phương pháp:
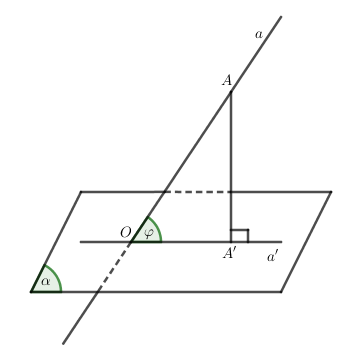
Để xác định góc giữa đường thẳng a và mặt phẳng (α) ta thực hiện theo các bước sau:
- Tìm giao điểm O=a∩(α)
- Dựng hình chiếu A′ của một điểm A∈a xuống (α)
- Góc ^AOA′=φ chính là góc giữa đường thẳng a và (α).
*) Để dựng hình chiếu A′ của điểm A trên (α) ta chọn một đường thẳng b⊥(α) khi đó AA′//b.
- Để tính góc φ ta sử dụng hệ thức lượng trong tam giác vuông ΔOAA′.
Ngoài ra, nếu không xác định góc φ thì ta có thể tính góc giữa đường thẳng a và mặt phẳng (α) theo công thức sinφ=|→u.→n||→u||→n| trong đó →u là VTCP của a còn →n là vec tơ có giá vuông góc với (α).

