1. Định nghĩa
- Khoảng cách từ điểm MM đến đường thẳng ΔΔ là khoảng cách giữa hai điểm MM và HH, trong đó HH là hình chiếu của điểm MM trên đường thẳng ΔΔ.
Kí hiệu: d(M,Δ)=MHd(M,Δ)=MH trong đó HH là hình chiếu của MM trên ΔΔ.
2. Bài toán tính khoảng cách từ một điểm đến một đường thẳng
Phương pháp:
Để tính khoảng cách từ điểm MM đến đường thẳng ΔΔ ta cần xác định được hình chiếu HH của điểm MM trên đường thẳng ΔΔ, rồi xem MHMH là đường cao của một tam giác nào đó để tính.
Điểm HH thường được dựng theo hai cách sau:
Cách 1: Trong mp(M,Δ)mp(M,Δ) vẽ MH⊥Δ⇒d(M,Δ)=MHMH⊥Δ⇒d(M,Δ)=MH
Cách 2: Dựng mặt phẳng (α)(α) qua MM và vuông góc với ΔΔ tại HH.
Khi đó d(M,Δ)=MHd(M,Δ)=MH.
Hai công thức sau thường được dùng để tính MHMH
CT1: ΔMABΔMAB vuông tại MM và có đường cao MHMH thì 1MH2=1MA2+1MB21MH2=1MA2+1MB2.
CT2: MHMH là đường cao của ΔMABΔMAB thì MH=2SMABABMH=2SMABAB.
Ví dụ: Cho hình chóp tam giác S.ABCS.ABC với SASA vuông góc với (ABC)(ABC) và SA=3a.SA=3a. Diện tích tam giác ABCABC bằng 2a2,BC=a2a2,BC=a. Khoảng cách từ SS đến BCBC bằng bao nhiêu?
A. 2a.2a. B. 4a.4a.
C. 3a.3a. D. 5a.5a.
Hướng dẫn giải:
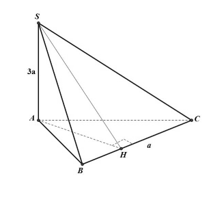
Kẻ AHAH vuông góc với BC:BC: SΔABC=12AH.BC⇒AH=2.SΔABCBC=4a2a=4aSΔABC=12AH.BC⇒AH=2.SΔABCBC=4a2a=4a
Ta có: SA⊥(ABC)⇒SA⊥BCSA⊥(ABC)⇒SA⊥BC
Lại có AH⊥BCAH⊥BC nên BC⊥(SAH)⇒BC⊥SHBC⊥(SAH)⇒BC⊥SH
Do đó khoảng cách từ SS đến BCBC chính là SH.SH.
Dựa vào tam giác vuông ΔSAHΔSAH ta có SH=√SA2+AH2=√(3a)2+(4a)2=5aSH=√SA2+AH2=√(3a)2+(4a)2=5a

