Bài toán:
Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(O\) và vuông góc với đường thẳng \(d\).
Phương pháp:
Cách 1: Tìm tất cả các đường thẳng vuông góc với \(d\), khi đó \(\left( \alpha \right)\) sẽ song song hoặc chứa các đường thẳng này và ta chuyển về dạng thiết diện song song như đã biết.
Cách 2: Ta dựng mặt phẳng \(\left( \alpha \right)\) như sau:
- Dựng hai đường thẳng \(a,b\) cắt nhau cùng vuông góc với \(d\), trong đó có một đường thẳng đi qua \(O\).
- Khi đó mặt phẳng \(\left( \alpha \right)\) chính là mặt phẳng \(\left( {a,b} \right)\).
Ví dụ: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều, \(SA \bot \left( {ABC} \right)\). Gọi $\left( P \right)$ là mặt phẳng qua $B$ và vuông góc với $SC$. Thiết diện của $\left( P \right)$ và hình chóp $S.ABC$ là:
A. Hình thang vuông.
B. Tam giác đều.
C. Tam giác cân.
D. Tam giác vuông.
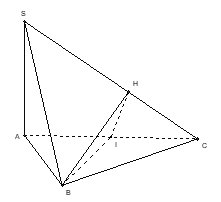
Giải:
Gọi \(I\) là trung điểm của \(AC\), kẻ \(IH \bot SC\).
Ta có \(BI \bot AC,\,BI \bot SA \Rightarrow BI \bot SC\).
Do đó \(SC \bot \left( {BIH} \right)\) hay thiết diện là tam giác \(BIH\).
Mà \(BI \bot \left( {SAC} \right)\) nên \(BI \bot IH\) hay thiết diện là tam giác vuông.
Chọn D.
