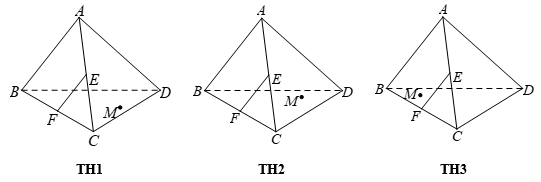
1. Các cách xác định mặt phẳng
Một mặt phẳng trong không gian có thể được xác định bởi một trong các cách thức sau:
- Mặt phẳng đó đi qua 3 điểm không thẳng hàng \(A,B,C\). Kí hiệu là mp\(\left( {ABC} \right)\).
- Mặt phẳng đó đi qua một đường thẳng \(a\)và một điểm \(A\) không thuộc đường thẳng \(a\). Kí hiệu mp\((A,a)\).
- Mặt phẳng đó đi qua hai đường thẳng cắt nhau \(a\) và \(b\). Kí hiệu, mp\(\left( {a,b} \right)\).
- Mặt phẳng đó đi qua hai đường thẳng song song \(a\),\(b\).
2. Phương pháp chứng minh ba điểm thẳng hàng, ba đường thẳng đồng quy
a) Để chứng minh ba điểm (hay nhiều điểm) thẳng hàng ta chứng minh chúng là điểm chung của hai mặt phẳng phân biệt, khi đó chúng nằm trên đường thẳng giao tuyên của hai mặt phẳng nên thẳng hàng. Tức là:
- Tìm $d = (\alpha ) \cap (\beta )$;
- Chỉ ra (chứng minh) $d$ đi qua ba điểm $A,B,C$ $ \Rightarrow A,B,C$ thẳng hàng.
Hoặc chứng minh đường thẳng $AB$ đi qua $C$ $ \Rightarrow A,B,C$ thẳng hàng.
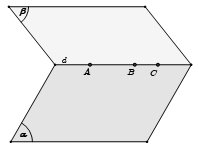
b) Để chứng minh ba đường thẳng đồng qui ta chứng minh giao điểm của hai đường thẳng thuộc đường đường thẳng còn lại.
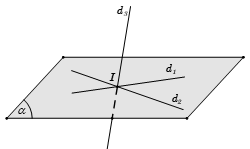
Phương pháp 1
Cơ sở của phương pháp này là ta cần chứng minh đường thẳng thứ nhất qua giao điểm của hai đường thẳng còn lại.
- Bước 1: Tìm $I = {d_1} \cap {d_2}$.
- Bước 2: Chứng minh ${d_3}$ đi qua $I$.
$ \Rightarrow {d_1},{d_2},{d_3}$ đồng quy tại $I$.
Phương pháp 2
Cơ sở của phương pháp là ta cần chứng minh chúng đôi một cắt nhau và dôi một ở trong ba mặt phẳng phân biệt.
- Bước 1: Xác định $\left\{ \begin{array}{l}{d_1},{d_2} \subset (\alpha );\,\,\,{d_1} \cap {d_2} = {I_1}\\{d_2},{d_3} \subset (\beta );\,\,\,{d_2} \cap {d_3} = {I_2}\\{d_3},{d_1} \subset (\gamma );\,\,\,{d_3} \cap {d_1} = {I_3}\end{array} \right.$ trong đó $(\alpha )$, $(\beta )$, $(\gamma )$ phân biệt
- Bước 2: Kết luận ${d_1},{d_2},{d_3}$ đồng quy tại $I \equiv {I_1} \equiv {I_2} \equiv {I_3}$.
Phương pháp 3:
- Chứng minh $a,b,c$ lần lượt là giao tuyến của hai trong ba mặt phẳng $\left( \alpha \right),\left( \beta \right),\left( \delta \right)$ trong đó có hai giao tuyến cắt nhau.
- Khi đó theo tính chất về giao tuyến của ba mặt phẳng ta được $a,b,c$ đồng qui.
3. Quan hệ song song giữa các đường thẳng, mặt phẳng trong không gian
a. Hai đường thẳng song song
- Là hai đường thẳng cùng thuộc một mặt phẳng nhưng không có điểm chung.
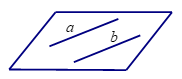
- Các cách chứng minh hai đường thẳng song song
C1. Chứng minh 2 đường thẳng đó đồng phẳng, rồi áp dụng phương pháp chứng minh song song trong hình học phẳng (như tính chất đường trung bình, định lí Talét đảo, …)
C2. Chứng minh 2 đường thẳng đó cùng song song với đường thẳng thứ ba.
C3. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
C4. Áp dụng định lí về giao tuyến song song.
b. Đường thẳng song song mặt phẳng
- Đường thẳng \(d\) và mặt phẳng \(\left( \alpha \right)\) không có điểm chung. Trong trường hợp này ta nói đường thẳng \(d\) song song với mặt phẳng \(\left( \alpha \right)\), kí hiệu \(d//\left( \alpha \right)\) .
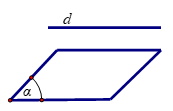
- Các tính chất:
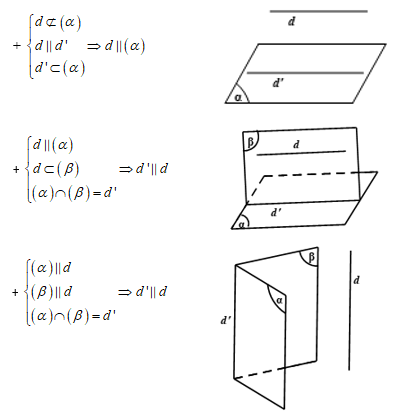
+ Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
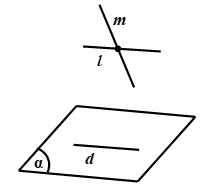
- Chứng minh đường thẳng song song mặt phẳng
Phương pháp 1
Cơ sở của phương pháp là dùng điều kiện cần và đủ để chứng minh đường thẳng $d$ song song với mặt phẳng $(\alpha )$.
- Bước 1: Quan sát và quản lí giả thiết tìm đường thẳng ưu việt $\Delta \subset (\alpha )$ và chứng minh $d\parallel \Delta $.
- Bước 2: Kết luận $d\parallel (\alpha )$.
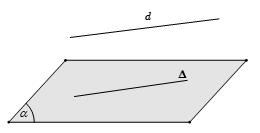
Phương pháp 2
Cơ sở của phương pháp là dùng định lý phương giao tuyến song song.
- Bước 1: Chứng minh $d = (\beta ) \cap (\gamma )$ mà $\left\{ \begin{array}{l}(\beta ) \cap (\alpha ) = a\\(\gamma ) \cap (\alpha ) = b\\a\parallel b\end{array} \right.$
- Bước 2: Kết luận $d\parallel (\alpha )$.
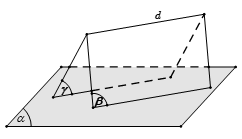
c. Mặt phẳng song song mặt phẳng
- Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không có điểm chung. Trong trường hợp này ta nói các mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\)song song với nhau, kí hiệu \(\left( \alpha \right)//\left( \beta \right)\) .
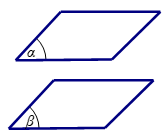
- Các định lí
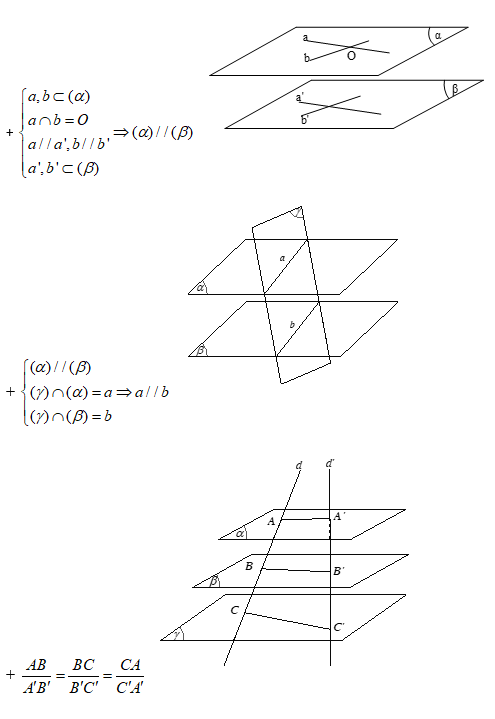
- Chứng minh hai mặt phẳng song song
Phương pháp 1
Cơ sở của phương pháp chứng minh hai mặt phẳng $(\alpha )$ và $(\beta )$ song song nhau là:
- Bước 1: Chứng minh mặt phẳng $(\alpha )$ chứa hai đường thẳng $a,b$ cắt nhau lần lượt song song với hai đường thẳng $a',b'$ cắt nhau trong mặt phẳng $(\beta )$.
- Bước 2: Kết luận $(\alpha )\parallel (\beta )$ theo điều kiện cần và đủ.
Phương pháp 2
- Bước 1: Tìm hai đường thẳng $a,b$ cắt nhau trong mặt phẳng $(\alpha )$.
- Bước 2: Lần lượt chứng minh $a\parallel (\beta )$ và $b\parallel (\beta )$
- Bước 3: Kết luận $(\alpha )\parallel (\beta )$.
4. Phương pháp xác định thiết diện
a. Thiết diện đi qua ba điểm không thẳng hàng
Phương pháp:
Để xác định thiết diện của hình chóp $S.{A_1}{A_2}...{A_n}$ cắt bởi mặt phẳng $\left( \alpha \right)$, ta tìm giao điểm của mặt phẳng $\left( \alpha \right)$ với các đường thẳng chứa các cạnh của hình chóp. Thiết diện là đa giác có đỉnh là các giao điểm của $\left( \alpha \right)$ với hình chóp (và mỗi cạnh của thiết diện phải là một đoạn giao tuyến với một mặt của hình chóp)
b. Thiết diện song song với đường thẳng
Phương pháp:
Sử dụng định nghĩa và các tính chất hoặc biểu thức tọa độ của phép tịnh tiến.
Trong phần này ta sẽ xét thiết diện của mặt phẳng $\left( \alpha \right)$ đi qua một điểm song song với hai đường thẳng chéo nhau hoặc $\left( \alpha \right)$ chứa một đường thẳng và song song với một đường thẳng; để xác định thiết diện loại này ta sử dụng tính chất: $\left\{ \begin{array}{l}\left( \alpha \right)\parallel d\\d \subset \left( \beta \right)\\M \in \left( \alpha \right) \cap \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( \beta \right) = d'\parallel d,M \in d'$
c. Thiết diện song song với mặt phẳng
Phương pháp:
- Để xác định thiết diện trong trường hợp này ta sử dụng các tính chất sau.
- Khi $\left( \alpha \right)\parallel \left( \beta \right)$ thì $\left( \alpha \right)$ sẽ song song với tất cả các đường thẳng trong $\left( \beta \right)$ và ta chuyển về dạng thiết diện song song với đường thẳng.
Sử dụng $\left\{ \begin{array}{l}\left( \alpha \right)\parallel \left( \beta \right)\\\left( \beta \right) \cap \left( \gamma \right) = d\\M \in \left( \alpha \right) \cap \left( \gamma \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( \gamma \right) = d'\parallel d,M \in d'$.
- Tìm đường thẳng $d$ nằm trong $\left( \beta \right)$ và xét các mặt phẳng có trong hình chóp mà chứa $d$, khi đó $\left( \alpha \right)\parallel d$ nên sẽ cắt các mặt phẳng chứa $d$( nếu có) theo các giao tuyến song song với $d$.
