1. Hàm số tuần hoàn
Hàm số \(y = f\left( x \right)\) có TXĐ \(D\) được gọi là hàm số tuần hoàn nếu có số \(T \ne 0\) sao cho:
a) \(\forall x \in D\) đều có \(x - T \in D,x + T \in D\).
b) \(\forall x \in D\) đều có \(f\left( {x + T} \right) = f\left( x \right)\).
Số \(T > 0\) nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn \(y = f\left( x \right)\).
2. Các hàm số lượng giác
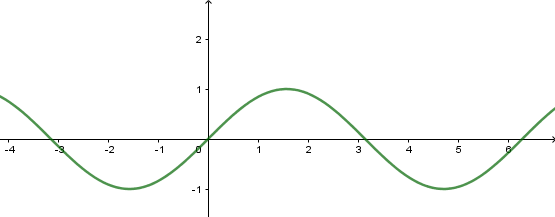
a) Hàm số \(y = \sin x\)
- Có TXĐ \(D = R\), là hàm số lẻ, tuần hoàn với chu kì \(2\pi \), nhận mọi giá trị thuộc đoạn \(\left[ { - 1;1} \right]\).
- Đồng biến trên mỗi khoảng \(\left( { - \dfrac{\pi }{2} + k2\pi ;\dfrac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\dfrac{\pi }{2} + k2\pi ;\dfrac{{3\pi }}{2} + k2\pi } \right)\).
- Có đồ thị là đường hình sin đi qua điểm \(O\left( {0;0} \right)\)
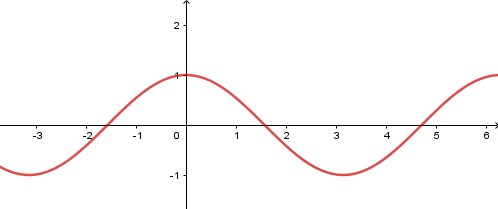
b) Hàm số \(y = \cos x\)
- Có TXĐ \(D = R\), là hàm số chẵn, tuần hoàn với chu kì \(2\pi \), nhận mọi giá trị thuộc đoạn \(\left[ { - 1;1} \right]\).
- Đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\)
- Có đồ thị là đường hình sin đi qua điểm \(\left( {0;1} \right)\)
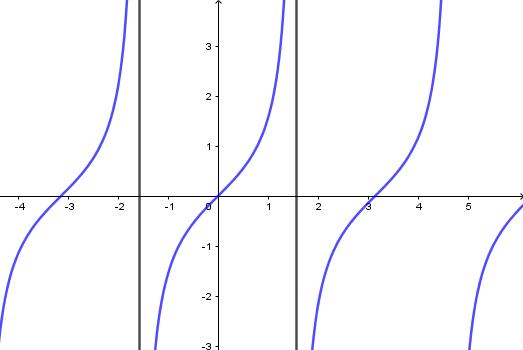
c) Hàm số \(y = \tan x\)
- Có TXĐ \(D = R\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}\), là hàm số lẻ, tuần hoàn với chu kì \(\pi \), nhận mọi giá trị thuộc \(R\).
- Đồng biến trên mỗi khoảng \(\left( { - \dfrac{\pi }{2} + k\pi ;\dfrac{\pi }{2} + k\pi } \right)\).
- Đồ thị nhận mỗi đường thẳng \(x = \dfrac{\pi }{2} + k\pi \) làm đường tiệm cận.
d) Hàm số \(y = \cot x\)
- Có TXĐ \(D = R\backslash \left\{ {k\pi ,k \in Z} \right\}\), là hàm số lẻ, tuần hoàn với chu kì \(\pi \), nhận mọi giá trị thuộc \(R\).
- Nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\).
- Đồ thị nhận mỗi đường thẳng \(x = k\pi \) làm đường tiệm cận.
3. Một số dạng toán thường gặp
Dạng 1: Tìm TXĐ của hàm số.
Phương pháp:
Sử dụng điều kiện xác định của các hàm phân thức, hàm căn bậc, hàm lượng giác (tan, cot).
- Hàm số \(y = \sqrt {f\left( x \right)} \) xác định nếu \(f\left( x \right) \ge 0\).
- Hàm số \(y = \dfrac{1}{{f\left( x \right)}}\) xác định nếu \(f\left( x \right) \ne 0\).
- Hàm số \(y = \tan u\left( x \right)\) xác định nếu \(\cos u\left( x \right) \ne 0 \Leftrightarrow u\left( x \right) \ne \dfrac{\pi }{2} + k\pi \).
- Hàm số \(y = \cot u\left( x \right)\) xác định nếu \(\sin u\left( x \right) \ne 0 \Leftrightarrow u\left( x \right) \ne k\pi \).
Dạng 2: Tìm chu kì của hàm số.
- Hàm số \(y = \sin \left( {ax + b} \right),y = \cos \left( {ax + b} \right)\) tuần hoàn với chu kỳ \(T = \dfrac{{2\pi }}{{\left| a \right|}}\).
- Hàm số \(y = \tan \left( {ax + b} \right),y = \cot \left( {ax + b} \right)\) tuần hoàn với chu kỳ \(T = \dfrac{\pi }{{\left| a \right|}}\).
- Hàm số \(y = {f_1}\left( x \right),y = {f_2}\left( x \right)\) lần lượt có chu kỳ \({T_1},{T_2}\) thì hàm số \(y = {f_1}\left( x \right) \pm {f_2}\left( x \right)\) có chu kỳ \({T_0} = BCNN\left( {{T_1},{T_2}} \right)\)
Dạng 3: Tìm GTLN, GTNN của hàm số lượng giác.
Phương pháp:
Sử dụng các đánh giá \( - 1 \le \sin x \le 1; - 1 \le \cos x \le 1\) để đánh giá tập giá trị của hàm số.
Khi tìm GTNN, GTLN cần xét điều kiện dấu “=” xảy ra.
