1. Định nghĩa
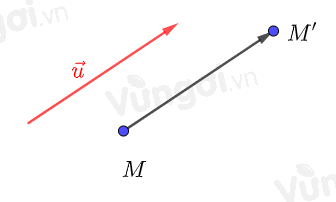
Phép đặt tương ứng mỗi điểm M với một điểm M′ sao cho →MM′=→u (→u là một véc tơ cố định) gọi là phép tịnh tiến theo véc tơ →u.
2. Tính chất
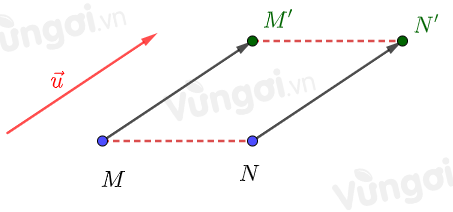
+) Nếu phép tịnh tiến biến hai điểm bất kì M,N thành hai điểm M′,N′ thì MN=M′N′.
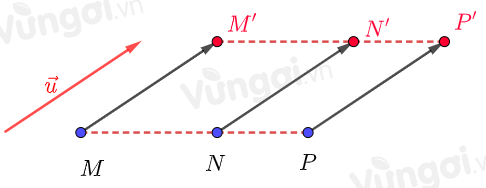
+) Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó.
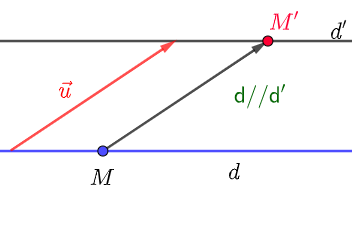
+) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
d song song với d':
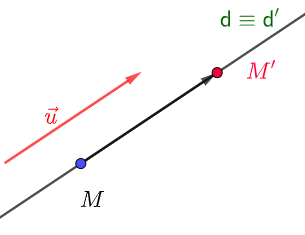
d trùng d':
+) Phép tịnh tiến biến tia thành tia, đoạn thẳng thành đoạn thẳng có độ dài bằng nó, góc thành góc có số đo bằng nó, tam giác thành tam giác bằng nó, đường tròn thành đường tròn có bán kính bằng nó.
3. Biểu thức tọa độ của phép tịnh tiến
Cho điểm M(x;y) và véc tơ →u=(a;b). Phép tịnh tiến theo véc tơ →u biến M thành M′(x′;y′) thỏa mãn:
{x′=x+ay′=y+b

