I. CÁC HÀM SỐ LƯỢNG GIÁC
1. Hàm số tuần hoàn
Hàm số $f\left( x \right)$ xác định trên tập hợp $D$ gọi là tuần hoàn nếu tồn tại một số dương $T$ sao cho với mọi $x \in D$ ta có:
+) $x - T \in D$ và $x + T \in D$
+) $f\left( {x + T} \right) = f\left( x \right)$
Số nhỏ nhất (nếu có) trong các số $T$ có các tính chất trên gọi là chu kì của hàm tuần hoàn $f\left( x \right).$
2. Các hàm số lượng giác
a) Hàm số $y = \sin x$
+ TXĐ: \(D = \mathbb{R}\)
+ Tập giá trị \(\left[ { - 1;1} \right]\)
+ Hàm số $y = \sin x$ là hàm số lẻ trên \(\mathbb{R}\).
+ Hàm số $y = \sin x$ tuần hoàn với chu kì $2\pi $
Chiều biến thiên trên \(\left[ { - \pi ;\pi } \right]\)
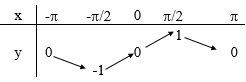
Đồ thị:
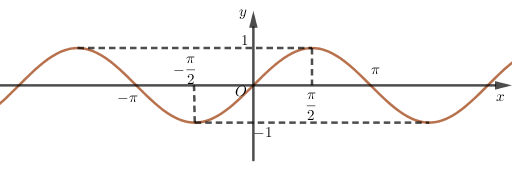
b) Hàm số \(y = \cos x\)
+ Hàm số \(y = \cos x\) là hàm số chẵn trên \(\mathbb{R}\).
+ Hàm số \(y = \cos x\) tuần hoàn với chu kì $2\pi $.
Chiều biến thiên trên \(\left[ { - \pi ;\pi } \right]\)
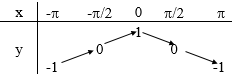
Đồ thị:
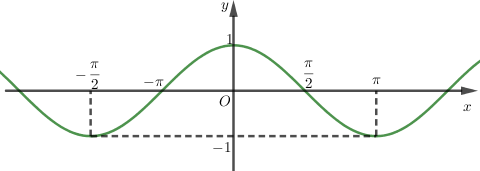
c) Hàm số \(y = \tan x\)
+ Hàm số \(y = \tan x\) là hàm số lẻ trên \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)
+ Hàm số \(y = \tan x\) tuần hoàn với chu kì \(\pi \).
Chiều biến thiên trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\)
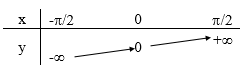
Đồ thị:
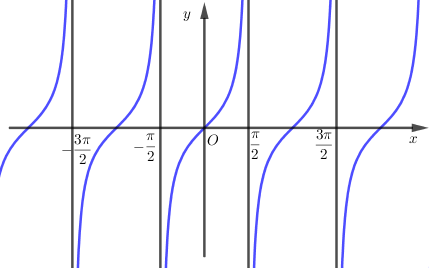
Chú ý: Trong hệ trục toạ độ $Oxy$ các đường thẳng có phương trình \(x = \dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}\) được gọi là các đường tiệm cận của đồ thị hàm số \(y = \tan x\).
d) Hàm số \(y = \cot x\)
+ Hàm số \(y = \cot x\) là hàm số lẻ trên \(\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\)
+ Hàm số \(y = \cot x\) tuần hoàn với chu kì \(\pi \).
Chiều biến thiên trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\)
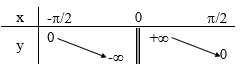
Đồ thị:
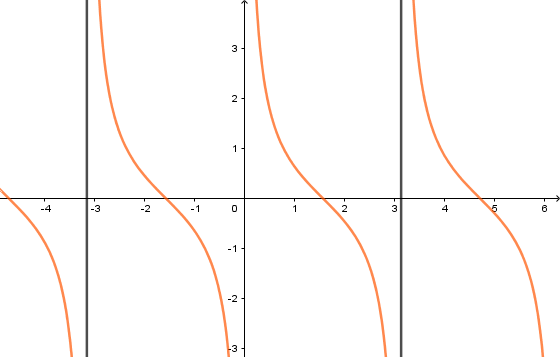
Chú ý: Trong hệ trục toạ độ $Oxy$ các đường thẳng có phương trình \(x = k\pi ,\;k \in \mathbb{Z}\) được gọi là các đường tiệm cận của đồ thị hàm số \(y = \cot x\)
II. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
1. Phương trình \(\sin x = m\)
+ Nếu $\left| m \right| > 1$ phương trình vô nghiệm.
+ Nếu $\left| m \right| \le 1$, khi đó đặt $m = \sin \alpha $ ta được: $\sin x = {\rm{sin}}\alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + 2k\pi \\x = \pi - \alpha + 2k\pi \end{array} \right.,k \in Z$
Đặc biệt: Ta có các kết quả:
\( + )\sin x = 0 \Leftrightarrow x = k\pi ;\)
\( + )\sin x = - 1 \Leftrightarrow x = - \dfrac{\pi }{2} + k2\pi ;\)
\( + )\sin x = 1 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi ;\)
2. Phương trình \(\cos x = m\)
+ Nếu $\left| m \right| > 1$ phương trình vô nghiệm.
+ Nếu $\left| m \right| \le 1$, khi đó đặt $m = \cos \alpha $ ta được: $\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + 2k\pi \\x = - \alpha + 2k\pi \end{array} \right.,k \in Z$
Đặc biệt: Ta có các kết quả:
\(\cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi ;\)\(\cos x = - 1 \Leftrightarrow x = \pi + k2\pi ;\)\(\cos x = 1 \Leftrightarrow x = k2\pi \)
3. Phương trình \(\tan x = m\)
Phương trình luôn có nghiệm \(x = \arctan m + k\pi \).
Đặc biệt: \(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in Z} \right)\)
4. Phương trình \(\cot x = m\)
Phương trình luôn có nghiệm \(x = {\mathop{\rm arccot}\nolimits} m + k\pi \).
Đặc biệt: \(\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in Z} \right)\).
III. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC ĐƠN GIẢN
1. Phương trình bậc nhất đối với một hàm số lượng giác
Chuyển phương trình về dạng phương trình lượng giác cơ bản.
2. Phương trình bậc hai đối với một hàm số lượng giác
Đặt hàm số lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ nếu có (thí dụ t = sinx hoặc t = cosx, điều kiện ½t½ £ 1), rồi giải phương trình theo ẩn phụ này.
3. Phương trình bậc nhất đối với \(\sin x\) và \(\cos x\)
Phương trình bậc nhất đối với \(\sin x\) và \(\cos x\) có dạng:
\(a\sin x + b\cos x = c\) (1)
Phương pháp chung:
Cách 1: (Thường dùng cho giải phương trình)
- Bước 1: Kiểm tra điều kiện có nghiệm của phương trình: \({a^2} + {b^2} \ge {c^2}\).
- Bước 2: Chia hai vế của phương trình cho \(\sqrt {{a^2} + {b^2}} \) thì phương trình có dạng:
\(\dfrac{a}{{\sqrt {{a^2} + {b^2}} }}\cos x + \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}\sin x = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\).
- Bước 3: Đặt \(\cos \alpha = \dfrac{a}{{\sqrt {{a^2} + {b^2}} }},\sin \alpha = \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}\) thì phương trình trở thành \(\cos \left( {x - \alpha } \right) = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\).
- Bước 4: Giải phương trình lượng giác cơ bản trên tìm \(x\).
Cách 2: (Thường dùng để giải và biện luận):
- Bước 1: Xét \(x = \pi + k2\pi \Leftrightarrow \dfrac{x}{2} = \dfrac{\pi }{2} + k\pi \) có là nghiệm hay không.
- Bước 2: Xét \(x \ne \pi + k2\pi \Leftrightarrow \dfrac{x}{2} \ne \dfrac{\pi }{2} + k\pi \) thì đặt \(t = \tan \dfrac{x}{2} \Rightarrow \sin x = \dfrac{{2t}}{{1 + {t^2}}},\cos x = \dfrac{{1 - {t^2}}}{{1 + {t^2}}}\) ta được phương trình bậc hai theo \(t:\left( {b + c} \right){t^2} - 2at + c - b = 0\).
- Bước 3: Giải phương trình trên tìm \(t \Rightarrow x\) và kiểm tra điều kiện, kết luận nghiệm.
Nhận xét :
Từ cách giải 1 ta có được kết quả sau:
$ - \sqrt {{a^2} + {b^2}} \le a\sin x + b\cos x \le \sqrt {{a^2} + {b^2}} $
Kết quả đó gợi ý cho bài toán về giá trị lớn nhất và nhỏ nhất của các hàm số dạng $y = a\sin x + b\cos x$ hoặc $y = \dfrac{{a.\sin x + b.\cos x}}{{c.\sin x + d.\cos x}}$ và phương pháp đánh giá cho một số phương trình lượng giác.
Dạng đặc biệt: Ta có các kết quả:
\(\begin{array}{l}\sin x + \cos x = 0 \Leftrightarrow x = - \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\\\sin x - \cos x = 0 \Leftrightarrow x = \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\end{array}\)
4. Phương trình đẳng cấp đối với \(\sin x\) và \(\cos x\)
Phương trình dạng \({a_0}{\sin ^n}x + {a_1}{\sin ^{n - 1}}x\cos x + ... + {a_{n - 1}}\sin x{\cos ^{n - 1}}x + {a_n}{\cos ^n}x = 0\).
Phương pháp chung:
- Bước 1: Xét \(\cos x = 0 \Rightarrow \sin x = 1\), thay vào phương trình xem có thỏa mãn hay không.
- Bước 2: Xét \(\cos x \ne 0\), chia hai vế của phương trình cho \({\cos ^n}x \ne 0\) và đặt \(\tan x = t\).
- Bước 3: Giải phương trình ẩn \(t\) tìm nghiệm \(t\).
- Bước 4: Giải phương trình \(\tan x = t\) tìm nghiệm, kiểm tra điều kiện và kết luận nghiệm.
5. Phương trình đối xứng và dạng đối xứng với \(\sin x\) và \(\cos x\)
Phương trình dạng \(a\left( {\sin x + \cos x} \right) + b\sin x\cos x + c = 0\).
Phương pháp chung:
- Bước 1: Đặt \(\sin x + \cos x = t \Rightarrow \sin x\cos x = \dfrac{{{t^2} - 1}}{2}\).
- Bước 2: Thay vào phương trình tìm \(t\).
- Bước 3: Giải phương trình \(\sin x + \cos x = t \Leftrightarrow \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right) = t\) để tìm \(x\).
