Góc giữa hai mặt phẳng

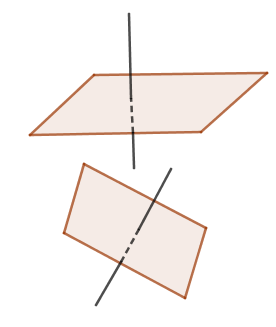
1. Định nghĩa

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

2. Cách xác định góc giữa hai mặt phẳng

TH1: Hai mặt phẳng $\left( P \right),\left( Q \right)$ song song hoặc trùng nhau thì góc giữa chúng bằng ${0^0}$.

TH2: Hai mặt phẳng $\left( P \right),\left( Q \right)$ không song song hoặc trùng nhau.

Cách 1:

+) Dựng hai đường thẳng $n,p$ lần lượt vuông góc với hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.

+) Khi đó, góc giữa hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ là góc giữa hai đường thẳng $n,p$.

Cách 2:

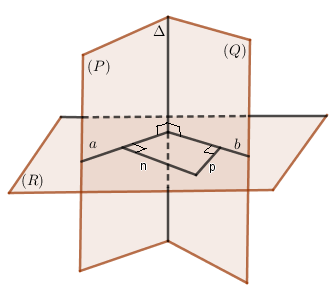
+) Xác định giao tuyến $\Delta$ của hai mặt phẳng $\left( P \right),\left( Q \right)$.

+) Tìm một mặt phẳng $\left( R \right)$ vuông góc $\Delta$ và cắt và hai mặt phẳng theo các giao tuyến $a,b$.

+) Góc giữa hai mặt phẳng $\left( P \right),\left( Q \right)$ là góc giữa $a$ và $b$.

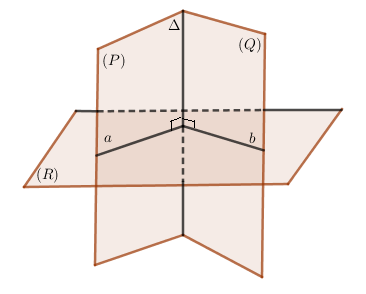
b) Diện tích hình chiếu của đa giác

Gọi $S$ là diện tích của đa giác $\left( H \right)$ trong $\left( P \right),S'$ là diện tích hình chiếu $\left( {H'} \right)$ của $\left( H \right)$ trên mặt phẳng $\left( Q \right)$ và $\alpha  = \left( {\left( P \right),\left( Q \right)} \right)$. Khi đó:

Ví dụ: Cho tứ diện $ABCD$ có $\Delta BCD$ vuông cân tại $B$, $AB \bot \left( {BCD} \right),BC = BD = a$, góc giữa $\left( {ACD} \right)$ và $\left( {BCD} \right)$ là ${30^0}$. Tính diện tích toàn phần của tứ diện $ABCD$.

Giải:

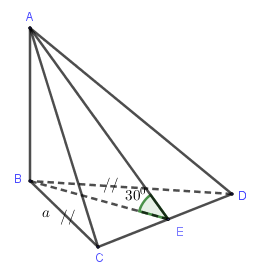
- Xác định góc giữa hai mặt phẳng $\left( {ACD} \right)$ và $\left( {BCD} \right)$:

Ta có: $\Delta ABC = \Delta ABC\left( {c.g.c} \right) \Rightarrow AC = AD$ (cạnh tương ứng)

Gọi $E$ là trung điểm của $CD \Rightarrow AE \bot CD,BE \bot CD$.

Ta có: $\left\{ \begin{array}{l}\left( {ACD} \right) \cap \left( {BCD} \right) = CD\\AE \bot CD\\BE \bot CD\end{array} \right.$  nên góc giữa hai mặt phẳng $\left( {ACD} \right)$ và $\left( {BCD} \right)$ là góc giữa hai đường thẳng $AE,BE$.

Do đó $\widehat {AEB} = {30^0}$.

- Tính diện tích toàn phần của tứ diện:

Tam giác vuông cân $BCE$ có:

$CD = \sqrt {B{C^2} + B{D^2}}  = a\sqrt 2  \Rightarrow BE = \dfrac{1}{2}CD = \dfrac{1}{2}.a\sqrt 2  = \dfrac{{a\sqrt 2 }}{2}$

Tam giác vuông $ABE$ có $AB = BE.\tan {30^0} = \dfrac{{a\sqrt 2 }}{2}.\dfrac{{\sqrt 3 }}{3} = \dfrac{{a\sqrt 6 }}{6}$

Do đó:

${S_{ABC}} = \dfrac{1}{2}BA.BC = \dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{6}.a = \dfrac{{{a^2}\sqrt 6 }}{{12}}$

${S_{ABD}} = \dfrac{1}{2}BA.BD = \dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{6}.a = \dfrac{{{a^2}\sqrt 6 }}{{12}}$

${S_{BCD}} = \dfrac{1}{2}BC.BD = \dfrac{{{a^2}}}{2}$

${S_{ACD}} = \dfrac{{{S_{BCD}}}}{{\cos {{30}^0}}} = \dfrac{1}{2}{a^2}:\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}}}{{\sqrt 3 }} = \dfrac{{{a^2}\sqrt 3 }}{3}$

Vậy diện tích toàn phần của tứ diện là:

$S = {S_{ABC}} + {S_{ABD}} + {S_{BCD}} + {S_{ACD}} = \dfrac{{{a^2}\sqrt 6 }}{{12}} + \dfrac{{{a^2}\sqrt 6 }}{{12}} + \dfrac{{{a^2}\sqrt 3 }}{3} + \dfrac{{{a^2}}}{2} = \dfrac{{{a^2}\left( {\sqrt 6  + 2\sqrt 3  + 3} \right)}}{6}$ .