Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(3a\), \(SA = SD = 3a\), \(SB = SC = 3a\sqrt 3 \). Gọi \(M\), \(N\) lần lượt là trung điểm của các cạnh \(SA\) và \(SD\), \(P\) là điểm thuộc cạnh \(AB\) sao cho \(AP = 2a\). Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( {MNP} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: d
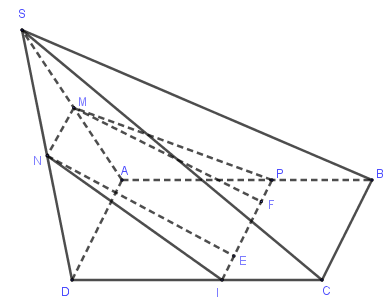
Do \(MN{\rm{//}}AD \Rightarrow MN{\rm{//}}BC\). Vậy \(\left( {MNP} \right)\) cắt mặt phẳng \(\left( {ABCD} \right)\) theo giao tuyến đi qua \(P\), song song \(BC\) và cắt \(DC\) tại điểm \(I\). Thiết diện của khối chóp cắt bởi mặt phẳng \(\left( {MNP} \right)\) chính là hình thang \(MNIP\).
Do \(\Delta NDI = \Delta MAP\) nên \(MP = NI\). Từ đó suy ra \(MNIP\) là hình thang cân.
Trong tam giác \(SAB\), ta có
\(\cos \widehat {SAB} = \dfrac{{S{A^2} + A{B^2} - S{B^2}}}{{2.SA.AB}} = \dfrac{{9{a^2} + 9{a^2} - 27{a^2}}}{{2.3a.3a}} = - \dfrac{{9{a^2}}}{{18{a^2}}} = - \dfrac{1}{2}\)
Trong tam giác\(MAP\), ta có \(M{P^2} = M{A^2} + A{P^2} - 2MA.AP.\cos \widehat {MAP} = \dfrac{{9{a^2}}}{4} + 4{a^2} + \dfrac{{3a}}{2} \cdot 2a = \dfrac{{37{a^2}}}{4} \Rightarrow MP = \dfrac{{a\sqrt {37} }}{2}\)
Từ \(M\) kẻ \(MF \bot PI\), từ \(N\) kẻ \(NE \bot PI\).
Dễ thấy, tứ giác \(MNEF\) là hình chữ nhật và từ đó suy ra \(MN = EF = \dfrac{{3a}}{2} \Rightarrow PF = EI = \dfrac{{3a}}{4}\)
Xét tam giác vuông \(MFP\), ta có \(MF = \sqrt {M{P^2} - F{P^2}} = \sqrt {\dfrac{{37{a^2}}}{4} - \dfrac{{9{a^2}}}{{16}}} = \dfrac{{a\sqrt {139} }}{4}\)
Ta có ${S_{MNIP}} = \dfrac{{\left( {MN + IP} \right).MF}}{2} = \dfrac{{\left( {\dfrac{{3a}}{2} + 3a} \right) \cdot \dfrac{{a\sqrt {139} }}{4}}}{2} = \dfrac{{9{a^2}\sqrt {139} }}{16}$
Hướng dẫn giải:
- Xác định thiết diện của hình chóp cắt bởi \(\left( {MNP} \right)\) và nhận xét hình dạng của thiết diện.
- Sử dụng kiến thức hình học phẳng để tính diện tích thiết diện tìm được.
