Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) có \(AB = 6\), \(CD = 8\). Cắt tứ diện bởi một mặt phẳng song song với \(AB\), \(CD\) để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng
Trả lời bởi giáo viên
Đáp án đúng: c
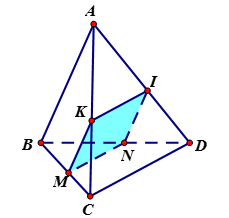
Giả sử một mặt phẳng song song với \(AB\) và \(CD\) cắt tứ diện \(ABCD\) theo một thiết diện là hình thoi \(MNIK\) như hình vẽ trên. Khi đó ta có: \(\left\{ \begin{array}{l}MK\,{\rm{//}}\,AB\,{\rm{//}}\,IN\\MN\,{\rm{//}}\,CD\,{\rm{//}}\,IK\\MK = KI\end{array} \right.\).
Cách 1: Theo định lí Ta – lét ta có: \(\left\{ \begin{array}{l}\dfrac{{MK}}{{AB}} = \dfrac{{CK}}{{AC}}\\\dfrac{{KI}}{{CD}} = \dfrac{{AK}}{{AC}}\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}\dfrac{{MK}}{6} = \dfrac{{AC - AK}}{{AC}}\\\dfrac{{KI}}{8} = \dfrac{{AK}}{{AC}}\end{array} \right.\)
\( \Rightarrow \dfrac{{MK}}{6} = 1 - \dfrac{{AK}}{{AC}}\)\( \Rightarrow \dfrac{{MK}}{6} = 1 - \dfrac{{KI}}{8}\)\( \Rightarrow \dfrac{{MK}}{6} = 1 - \dfrac{{MK}}{8}\)\( \Leftrightarrow \dfrac{7}{{24}}MK = 1\)\( \Leftrightarrow MK = \dfrac{{24}}{7}\).
Vậy hình thoi có cạnh bằng \(\dfrac{{24}}{7}\).
Hướng dẫn giải:
Dựng hình, sử dụng định lý Ta – lét trong hình học phẳng suy ra các tỉ lệ cạnh và tính toán.
