Cho hình chóp \(S.ABCD\) có đáy là hình vuông. Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(M\) là trung điểm của \(DO\), \(\left( \alpha \right)\) là mặt phẳng đi qua \(M\) và song song với $AC$ và $SD$. Thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) là hình gì.
Trả lời bởi giáo viên
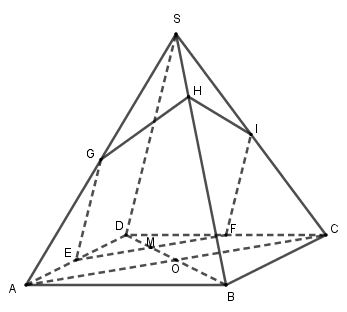
Dựng \(d\) qua \(M\) song song với \(AC\) và lần lượt cắt $AD$, $CD$ tại $E$, $F$.
\(d \cap AD = E\); \(d \cap CD = F\),
Dựng \({d_1}\) qua \(M\) song song với \(SD\) và lần lượt cắt $SA$, $SB$, $SC$ tại $G$, $H$, $I$.
Mặt phẳng \(\left( \alpha \right)\) cắt hình chóp tạo nên thiết diện là ngũ giác $EFIHG$.
Hướng dẫn giải:
Xác định giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp sử dụng quan hệ đường thẳng song song với mặt phẳng thì nó sẽ song song với một đường thẳng nào đó thuộc mặt phẳng.

