Câu hỏi:
2 năm trước
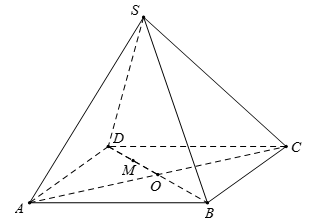
Cho hình chóp \(S.ABCD\), \(G\) là điểm nằm trong tam giác \(SCD\). \(E\), \(F\) lần lượt là trung điểm của \(AB\) và $AD$. Thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( {EFG} \right)\) là
Trả lời bởi giáo viên
Đáp án đúng: c
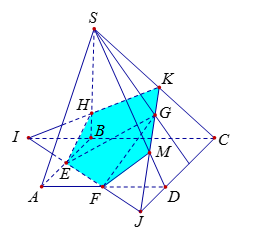
Trong mặt phẳng \(\left( {ABCD} \right):EF \cap BC = I;\)\(EF \cap CD = J\)
Trong mặt phẳng \(\left( {SCD} \right):GJ \cap SC = K;\)\(GJ \cap SD = M\)
Trong mặt phẳng \(\left( {SBC} \right):KI \cap SB = H\)
Ta có: \(\left( {GEF} \right) \cap \left( {ABCD} \right) = EF\), \(\left( {GEF} \right) \cap \left( {SAD} \right) = FM\), \(\left( {GEF} \right) \cap \left( {SCD} \right) = MK\)
$\left( {GEF} \right) \cap \left( {SBC} \right) = KH$, \(\left( {GEF} \right) \cap \left( {SAB} \right) = HE\)
Vậy thiết diện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \(\left( {EFG} \right)\) là ngũ giác $EFMKH$
Hướng dẫn giải:
Tìm các giao tuyến của \(\left( {EFG} \right)\) với các mặt của hình chóp rồi kết luận.
