Câu hỏi:
2 năm trước
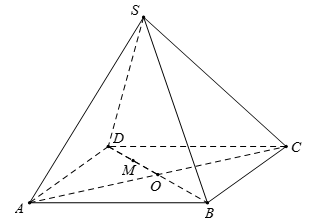
Cho tứ diện $ABCD$ có $AB = CD$ . Mặt phẳng \(\left( \alpha \right)\) qua trung điểm của $AC$ và song song với $AB,CD$ cắt $ABCD$ theo thiết diện là:
Trả lời bởi giáo viên
Đáp án đúng: c
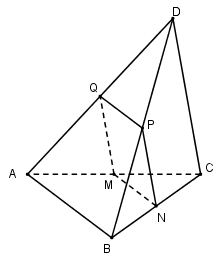
Gọi $M$ là trung điểm của $AC$ .
Trong $\left( {ABC} \right)$ qua $M$ kẻ \(MN//AB\left( {N \in BC} \right)\)
Trong $\left( {ACD} \right)$ và $\left( {BCD} \right)$ kẻ $MQ//CD$ và \(NP//CD\left( {Q \in AD,P \in BD} \right)\).
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ABC} \right)\\AB \subset \left( {ABC} \right)\\AB//\left( \alpha \right)\\MN//AB\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {ABC} \right) = MN.\)
Chứng minh tương tự ta có: \(\left( \alpha \right) \cap \left( {BCD} \right) = NP//CD\)
\(\begin{array}{l}\left( \alpha \right) \cap \left( {ABD} \right) = PQ//AB\\\left( \alpha \right) \cap \left( {ACD} \right) = QM//CD.\end{array}\)
Vậy thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) là tứ giác $MNPQ$ .
Ta có: $MN//PQ//AB,MQ//NP//CD$ nên $MNPQ$ là hình bình hành.
Ta có: $MN$ là đường trung bình của tam giác $ABC$ và $MQ$ là đường trung bình của tam giác $ACD$ nên \(MN = \dfrac{1}{2}AB,MQ = \dfrac{1}{2}CD.\)
Mà $AB = CD$ nên $MN = MQ$ . Vậy $MNPQ$ là hình thoi.
Hướng dẫn giải:
- Đưa về cùng mặt phẳng.
- Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung $M$ và lần lượt chứa hai đường thẳng song song $d$ và $d'$ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua $M$ và song song với $d$ và $d'$.
- Vận dụng các dấu hiệu nhận biết hình bình hành và hình thoi.
