Ôn tập chương 7: Mắt - Các dụng cụ quang

Thấu kính cho ảnh thật cao gấp 5 lần vật  \( \to k =  - 5 =  - \dfrac{{d'}}{d} \to d' = 5d\)

Lại có: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} \to \dfrac{1}{{15}} = \dfrac{1}{d} + \dfrac{1}{{5d}} \to \dfrac{1}{{15}} = \dfrac{6}{{5d}} \to d = 18cm\)

B- đúng vì vật thật qua thấu kính phân kì luôn cho ảnh ảo, cùng chiều và nhỏ hơn vật

Ta có:  f = - 10 cm = -0,1 m

\(D = \dfrac{1}{f} = \dfrac{1}{{ - 0,1}} =  - 10(dp)\)

Ta có:\(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} \to d = \dfrac{{fd'}}{{d' - f}};d' = \dfrac{{fd}}{{d - f}}\)

Lại có: \(k =  - \dfrac{{d'}}{d} \to k = \dfrac{f}{{f - d}};k = \dfrac{{f - d'}}{f}\)

\( \to \)A sai, B,C,D- đúng

Ta có vật thật đặt trước thấu kính cho ảnh trước thấu kính và gần thấu kính hơn vật \( \to \)thấu kính được sử dụng là thấu kính phân kì, ảnh thu được là ảnh ảo \( \to d' =  - 20cm\)

\(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{{40}} + \dfrac{1}{{ - 20}} = \dfrac{{ - 1}}{{40}} \to f =  - 40cm\)

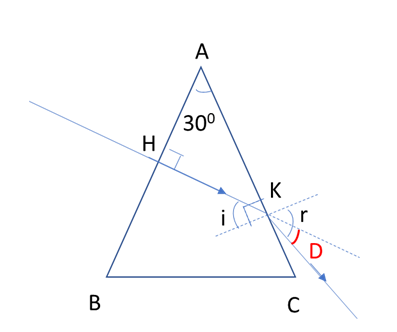
Tia sáng chiếu tới AB vuông góc tại H nên truyền thẳng tới AC tại K

Xét tam giác AHK vuông tại H có \(\widehat {\rm{A}}{\rm{ = 3}}{{\rm{0}}^{\rm{0}}} \to \widehat {{\rm{AKH}}} = 6{{\rm{0}}^{\rm{0}}} \to i = 3{{\rm{0}}^{\rm{0}}}\)(1)

Ta có, tại mặt bên AC: \(\sin {i_{gh}} = \dfrac{1}{n} = \dfrac{1}{{\sqrt 2 }} \to {i_{gh}} = {45^0}\)(2)

Từ (1) và (2): \(i < \sin {i_{gh}} \to \)tia sáng truyền tại mặt bên AC tại K bị khúc xạ ra ngoài không khí với góc lệch D như hình vẽ: D = r – i (3)

Áp dụng định luật khúc xạ ánh sáng tại mặt AC ta có: \(n.\sin i = {\mathop{\rm s}\nolimits} {\rm{inr}} \to \sqrt 2 \sin 30 = {\mathop{\rm s}\nolimits} {\rm{inr}} \to {\mathop{\rm s}\nolimits} {\rm{inr}} = \dfrac{{\sqrt 2 }}{2} \to r = {45^0}\)

Thay vào (3) \( \to D = {15^0}\)

Ta có: \({D_{\min }} = 2i - A \to i = ({D_{\min }} + A)/2 = {51^0}\)

Ta có: \(n = \dfrac{{\sin (\dfrac{{{D_{\min }} + A}}{2})}}{{\sin \dfrac{A}{2}}} = \dfrac{{\sin (\dfrac{{42 + 60}}{2})}}{{\sin \dfrac{{60}}{2}}} = \dfrac{{\sin 51}}{{\sin 30}}≈1,55\)

A – sai vì: Kính lúp là quang cụ có tác dụng làm tăng góc trông vật

B – sai vì: Kính lúp là quang cụ bổ trở cho mắt trong việc quan sát các vật nhỏ chứ không phải vật rất nhỏ (Vật rất nhỏ - ta dùng kính hiển vi)

C – đúng

D – sai vì: Kính lúp là thấu kính hội tụ bổ trợ cho mắt trong việc quan sát các vật nhỏ

Ta có: công thức tính độ bội giác của kính lúp: \({\rm{G  =  k}}{\rm{.}}\dfrac{D}{{\left| {d'} \right| + \ell }}\)

Trong đó: \(D = O{C_c}\); \(\ell \): khoảng cách từ mắt đến kính; d’: khoảng cách từ ảnh đến kính; \(k = \dfrac{{A'B'}}{{AB}}\): độ phóng đại ảnh cho bởi kính lúp

Khi ngắm chừng ở điểm cực cận: \(\left| {d'} \right| + \ell  = D \to G = k\)

Ta có công thức tính độ bội giác của kính lúp khi ngắm chừng ở vô cực: \(G = \dfrac{D}{f}\)

B- đúng

B- đúng vì kính hiển vi gồm một vật kính là thấu kính hội tụ có tiêu cự rất ngắn cỡ milimet và một thị kính là một thấu kính hội tụ có tiêu cự ngắn ( đóng vai trò kính lúp)

A- đúng vì

Ta có công thức tính độ bội giác của kính hiển vi khi ngắm chừng ở vô cực: \({G_\infty } = \left| {{k_1}} \right|.{G_2} = \dfrac{{\delta D}}{{{f_1}{f_2}}} \to \)khi ngắm chừng ở vô cực, độ bội giác của kính hiển vi tỉ lệ nghịch với tiêu cự của vật kính và thị kính

Gọi khoảng cách của vật tới thấu kính trước khi dịch chuyển là d, khoảng cách ảnh tới thấu kính là d’ ta có: \(\dfrac{1}{{{d_1}}} + \dfrac{1}{{{d_1}'}} = \dfrac{1}{f} = \dfrac{1}{{10}}\)(1)

Với thấu kính hội tụ khi dịch chuyển vật một khoảng 5 cm lại gần thấu kính thì ảnh sẽ dịch chuyển xa thấu kính hơn, theo đề bài ảnh dịch chuyển một khoảng là 10 cm nên ta có: \(\dfrac{1}{{{d_2}}} + \dfrac{1}{{{d_2}'}} = \dfrac{1}{f}\)

\(\to \dfrac{1}{{{d_1} - 5}} + \dfrac{1}{{{d_1}' + 10}} = \dfrac{1}{{10}}\)(2)

Từ (1) và (2) \( \to {d_1} = 20cm;{d_1}' = 20cm\)

Ta có: \(D = \dfrac{1}{f} \to f = \dfrac{1}{D} = \dfrac{1}{{10}} = 0,1(m) = 10(cm)\)

\(\dfrac{1}{f} = \dfrac{1}{{{d_1}}} + \dfrac{1}{{{d_1}'}} \to \dfrac{1}{{10}} = \dfrac{1}{6} + \dfrac{1}{{{d_1}'}} \to {d_1}' =  - 15'(cm)\)< 0, ảnh của S\(_1\)là ảnh ảo nằm trước thấu kính

Ảnh của S\(_2\)qua thấu kính trùng với ảnh của S\(_1\)nên S\(_2\)tạo ảnh thật \( \to {d_2}' = 15cm\)

\(\dfrac{1}{f} = \dfrac{1}{{{d_2}}} + \dfrac{1}{{{d_2}'}} \to \dfrac{1}{{10}} = \dfrac{1}{{{d_2}}} + \dfrac{1}{{15}} \to {d_2} = 30(cm)\)

\( \to \)khoảng cách giữa S\(_1\)và S\(_2\)là: 6 + 30 = 36 cm

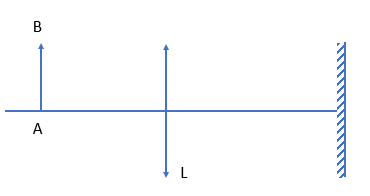
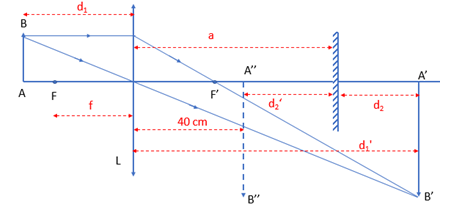
Ta có: \({d_1} = 80cm;f = 60cm;{d_2} = {d_2}' = a - 40cm\)

Sử dụng công thức thấu kính: \(\dfrac{1}{f} = \dfrac{1}{{{d_1}}} + \dfrac{1}{{{d_1}'}} \to \dfrac{1}{{60}} = \dfrac{1}{{80}} + \dfrac{1}{{{d_1}'}} \to {d_1}' = 240cm\)

Sử dụng công thức phản xạ qua gương phẳng: \({d_2}' = {d_2} = a - 40cm\)

Hình vẽ \( \to {d_1}' = 240cm = a + (a - 40) \to a = (240 + 40):2 = 140cm\)