Câu hỏi:
2 năm trước
Một tia sáng tới vuông góc với mặt AB của một lăng kính có chiết suất n=\(\sqrt 2 \)
và góc chiết quang A = 300. Góc lệch của tia sáng qua lăng kính là:
Trả lời bởi giáo viên
Đáp án đúng: c
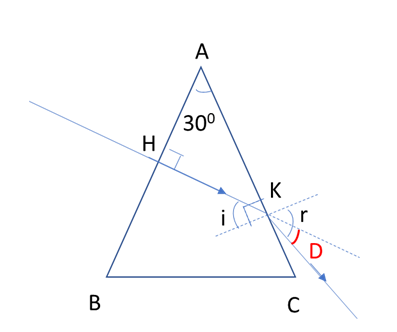
Tia sáng chiếu tới AB vuông góc tại H nên truyền thẳng tới AC tại K
Xét tam giác AHK vuông tại H có \(\widehat {\rm{A}}{\rm{ = 3}}{{\rm{0}}^{\rm{0}}} \to \widehat {{\rm{AKH}}} = 6{{\rm{0}}^{\rm{0}}} \to i = 3{{\rm{0}}^{\rm{0}}}\)(1)
Ta có, tại mặt bên AC: \(\sin {i_{gh}} = \dfrac{1}{n} = \dfrac{1}{{\sqrt 2 }} \to {i_{gh}} = {45^0}\)(2)
Từ (1) và (2): \(i < \sin {i_{gh}} \to \)tia sáng truyền tại mặt bên AC tại K bị khúc xạ ra ngoài không khí với góc lệch D như hình vẽ: D = r – i (3)
Áp dụng định luật khúc xạ ánh sáng tại mặt AC ta có: \(n.\sin i = {\mathop{\rm s}\nolimits} {\rm{inr}} \to \sqrt 2 \sin 30 = {\mathop{\rm s}\nolimits} {\rm{inr}} \to {\mathop{\rm s}\nolimits} {\rm{inr}} = \dfrac{{\sqrt 2 }}{2} \to r = {45^0}\)
Thay vào (3) \( \to D = {15^0}\)
Hướng dẫn giải:
Sử dụng định luật khúc xạ ánh sáng \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
