Chọn phát biểu đúng?
Hiện tượng dương cực tan xảy ra khi điện phân một dung dịch muối kim loại mà anốt làm bằng chính kim loại ấy
Bản chất của hiện tượng dương cực tan là
Bản chất của hiện tượng dương cực tan là cực dương của bình điện phân bị tác dụng hóa học tạo thành chất điện phân và tan vào dung dịch
Hiện tượng điện phân không ứng dụng để
Ứng dụng của hiện tượng điện phân gồm: Điều chế hóa chất, luyện kim, mạ điện
=> Hiện tượng điện phân không ứng dụng để sơn tĩnh điện
Công thức nào sau đây là công thức đúng của định luật Fa-ra-đây?
Biểu thức của định luật Fa-ra-đây: \(m = \frac{1}{F}\frac{A}{n}q = \frac{1}{F}\frac{A}{n}It \to I = \frac{{mFn}}{{At}}\)
Phát biểu nào sau đây là đúng?
Khi có hiện tượng dương cực tan, dòng điện trong chất điện phân tuân theo định luật Ôm
Phát biểu nào sau đây không đúng khi khi nói về cách mạ một huy chương bạc:
Khi mạ điện:
+ Vật cần được mạ dùng làm cực âm
+ Kim loại dùng để mạ làm cực dương
+ Chất điện phân là dung dịch muối của kim loại dùng để mạ
=> B - Đặt huy chương ở giữa anốt và catốt là sai
Khi điện phân dương cực tan, nếu tăng cường độ dòng điện và thời gian điện phân lên 2 lần thì khối lượng chất giải phóng ra ở điện cực.
Theo định luật Fa-ra-đây, ta có: \(m = \frac{1}{F}.\frac{A}{n}It\)
=> Khi tăng I và t lên hai lần thì khối lượng chất giải phóng ra ở điện cực sẽ tăng 4 lần
Khi điện phân dung dịch AgNO3 với cực dương là Ag biết khối lượng mol của bạc là 108. Cường độ dòng điện chạy qua bình điện phân để trong 1 h để có 27 gam Ag bám ở cực âm là
Ta có khối lượng bạc bám ở cực âm:
\(m = \frac{1}{F}.\frac{A}{n}It \to I = \frac{{mFn}}{{At}}\)
Với m = 27 gam, F = 96500 C.mol-1, n = 1, A = 108, t = 1 giờ = 3600s
\( \to I = \frac{{27.96500.1}}{{108.3600}}\, = \,6,7A\)
Điện phân cực dương tan một dung dịch trong 20 phút thì khối lượng cực âm tăng thêm 4 gam. Nếu điện phân trong một giờ với cùng cường độ dòng điện như trước thì khối lượng cực âm tăng thêm là
Ta có:
+ Khi điện phân trong thời gian t1 = 20 phút = 1200s: \({m_1} = 4g = \dfrac{{AI{t_1}}}{{Fn}}\)
+ Khi điện phân trong thời gian t2 = 1giờ = 3600s: \({m_2} = \dfrac{{AI{t_2}}}{{Fn}}\)
\(\dfrac{{{m_2}}}{{{m_1}}} = \dfrac{{{t_2}}}{{{t_1}}} = \dfrac{{3600}}{{1200}} = 3 \to {m_2} = 3{m_1} = 3.4 = 12\,g\)
Hai bình điện phân: (FeCl3/Fe và CuSO4/Cu) mắc nối tiếp. Sau một khoảng thời gian, bình thứ nhất giải phóng một lượng sắt là 1,4 g. Lượng đồng giải phóng ở bình thứ hai trong cùng khoảng thời gian đó là bao nhiêu ? Biết nguyên tử lượng của đồng và sắt là 64 và 56, hóa trị của đồng và sắt là 2 và 3.
Áp dụng công thức định luật Fa-ra-đây, ta có:
\({m_1} = \frac{{A_1I_1{t}}}{{Fn_1}}\) (1)
\({m_2} = \frac{{A_2I_2{t}}}{{Fn_2}}\) (2)
Do 2 bình mắc nối tiếp => I1 = I2= I. Chia (2) cho (1)
\(\frac{{{m_2}}}{{{m_1}}} = \frac{{\frac{{{A_2}}}{{{n_2}}}}}{{\frac{{{A_1}}}{{{n_1}}}}} \to {m_2} = \frac{{{m_1}{A_2}{n_1}}}{{{n_2}{A_1}}} = \frac{{1,4.64.3}}{{2.56}} = 2,4\,g\)
Một bộ nguồn điện gồm $30$ pin mắc thành $3$ nhóm nối tiếp, mỗi nhóm có $10$ pin mắc song song, mỗi pin có suất điện động $0,9V$ và điện trở trong \(0,6\Omega\). Một bình điện phân đựng dung dịch CuSO4 có điện trở \(205\Omega\) được mắc vào hai cực của bộ nguồn nói trên. Anốt của bình điện phân bằng đồng. Khối lượng đồng bám vào catốt của bình trong thời gian $50$ phút là? Biết đồng có $A = 64, n = 2$
Ta có:
- Suất điện động của bộ nguồn: Eb = 3E0 = 3.0,9 = 2,7V
- Điện trở trong của bộ nguồn: \({r_b} = 3\frac{r}{{10}} = 3.\frac{{0,6}}{{10}} = 0,18\Omega \)
- Cường độ dòng điện trong mạch: \(I = \frac{{{E_b}}}{{R + {r_b}}} = \frac{{2,7}}{{205 + 0,18}} = 0,01316\,A\)
- Khối lượng đồng bám vào catốt của bình trong thời gian 50 phút là:
\(m = \frac{1}{F}\frac{{AIt}}{n} = \frac{{64.0,01316.50.60}}{{96500.2}} = 0,0131g\)
Muốn mạ đồng một tấm sắt có diện tích tổng cộng $200cm^2$, người ta dùng tấm sắt làm catốt của một bình điện phân đựng dung dịch $CuSO_4$ và anốt là một thanh đồng nguyên chất, rồi cho dòng điện có cường độ $I = 10A$ chạy qua trong thời gian $2$ giờ $40$ phút $50$ giây. Bề dày lớp đồng bám trên mặt tấm sắt là bao nhiêu? Biết đồng có $A = 64$, $n = 2$ và có khối lượng riêng $ρ = 8,9.10^3 kg/m^3$
Ta có:
Khối lượng đồng bám vào tấm sắt: \(m = \dfrac{1}{F}\dfrac{A}{n}It = \dfrac{1}{{96500}}\dfrac{{64}}{2}10.(2.60.60 + 40.60 + 50) = 32g\)
Mặt khác, ta có: $m = ρSh$
\( \to h = \dfrac{m}{{\rho S}} = \dfrac{{{{32.10}^{ - 3}}}}{{8,{{9.10}^3}{{.200.10}^{ - 4}}}} = 1,{798.10^{ - 4}}m \approx 0,018cm\)
Đồ thị biểu diễn sự phụ thuộc giữa khối lượng chất giải phóng ra ở điện cực của bình điện phân và điện lượng tải qua bình
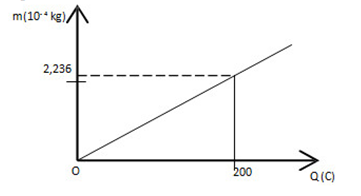
Đương lượng điện hóa của chất điện phân trong bình này là:
Theo định luật I - Faraday, ta có: m = kq
\( \to k = \frac{m}{q} = \frac{{2,{{236.10}^{ - 4}}}}{{200}} = 1,{118.10^{ - 6}}kg/C\)
Bình điện phân có anốt làm bằng kim loại của chất điện phân có hóa trị 2. Cho dòng điện 0,2A chạy qua bình trong 16 phút 5 giây thì có 0,064g chất thoát ra ở điện cực. Kim loại dùng làm anốt của bình điện phân là:
Ta có:
Khối lượng chất thoát ra ở điện cực:
\(m = \frac{1}{F}\frac{A}{n}It \leftrightarrow 0,064 = \frac{1}{{96500}}\frac{A}{2}.0,2.(16.60 + 5) \to A = 64\)
=> Kim loại dùng làm anot của bình điện phân là đồng có số khối A = 64
Cho mạch điện như hình vẽ:
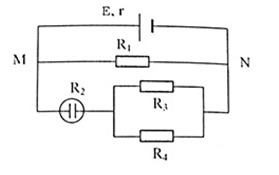
\(E = 13,5V, r = 1\Omega\), \({R_1} = 3\Omega\), \({R_3} = {R_4} = 4\Omega\). Bình điện phân dung dịch CuSO4, anot bằng đồng, có điện trở \({R_2}= 4\Omega\). Cường độ dòng điện qua bình điện phân có giá trị?
Mạch ngoài gồm:
R1 // [R2 nt (R3 // R4)]
\({R_{34}} = \dfrac{{{\rm{ }}{R_3}{R_4}}}{{{\rm{ }}{R_3} + {R_4}}} = {\rm{ }}\dfrac{{4.4}}{{4 + 4}} = 2\Omega \)
R234 = R2 + R34 = 4 + 2 = 6$\Omega $
Tổng trở tương đương mạch ngoài:
\(R = \dfrac{{{R_1}{R_{234}}}}{{{R_1} + {R_{234}}}} = \dfrac{{3.6}}{{3 + 6}} = 2\Omega \)
Áp dụng định luật Ôm cho toàn mạch, ta có:
\(I = \dfrac{E}{{R + r}} = \dfrac{{13,5}}{{2 + 1}} = 4,5A\)
Hiệu điện thế giữa M,N là: UMN = I.R = 4,5.2 = 9V
Cường độ dòng điện qua bình điện phân: \(I' = \dfrac{{{U_{MN}}}}{{{R_{234}}}} = \dfrac{9}{6} = 1,5A\)
Cho mạch điện như hình vẽ:
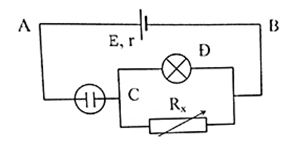
\(E = 9V; r = 0,5\Omega \). Bình điện phân chứa dung dịch đồng sunfat với hai cực bằng đồng. Đèn ghi \(6V - 9W\). \(R_x\) là một biến trở. Điều chỉnh \({R_x} = 12\Omega\) thì đèn sáng bình thường. Điện trở của bình điện phân là:
Ta có:
+ Điện trở của đèn: \({R_d} = \frac{{{U^2}}}{P} = \frac{{{6^2}}}{9} = 4\Omega \)
+ Cường độ dòng điện qua đèn: \({I_d} = \frac{P}{U} = \frac{9}{6} = 1,5A\)
+ Ud = URx = 6V
=> Cường độ dòng điện qua Rx: \({I_x} = \frac{{{U_{{R_x}}}}}{{{R_x}}} = \frac{6}{{12}} = 0,5A\)
Cường độ dòng điện chính trong mạch: I = Id + Ix = 1,5 + 0,5 = 2A
Mặt khác: \(I = \frac{E}{{{R_N} + r}} \to {R_N} = \frac{E}{I} - r = \frac{9}{2} - 0,5 = 4\Omega \)
Mạch ngoài gồm: Rb ( điện trở bình điện phân) nt (Rd // Rx)
\({R_{dx}} = \frac{{{R_d}{R_x}}}{{{R_d} + {R_x}}} = \frac{{4.12}}{{4 + 12}} = 3\Omega \)
\({R_N} = {\rm{ }}{R_b} + {\rm{ }}{R_{dx}} \to {R_b} = 4 - 3 = 1\Omega \)
Người ta dùng $36$ nguồn giống nhau, mỗi nguồn có suất điện động \({E_0} = 1,5V\), điện trở trong \(r = 0,9\Omega \) để cung cấp điện cho một bình điện phân đựng dung dịch ZnSO4 với cực dương bằng kẽm, có điện trở \(R = 3,6\Omega \). Mắc hỗn hợp đối xứng bộ nguồn sao cho dòng điện qua bình điện phân là lớn nhất. Tính lượng kẽm bám vào catốt của bình điện phân trong thời gian $1$ giờ $4$ phút $20$ giây. Biết kẽm có $A = 65, n = 2$.
Gọi x - là số nhánh
=> Số nguồn trên một nhánh là: \(y = \frac{{36}}{x}\)
Ta có:
+ Suất điện động của bộ nguồn: \({E_b} = y{E_0} = \frac{{36}}{x}{E_0} = \frac{{54}}{x}\)
+ Điện trở trong của bộ nguồn: \({r_b} = \frac{{yr}}{x} = \frac{{\frac{{36}}{x}.0,9}}{x} = \frac{{32,4}}{{{x^2}}}\)
Cường độ dòng điện qua mạch: \(I = \frac{{{E_b}}}{{R + {r_b}}} = \frac{{\frac{{54}}{x}}}{{3,6 + \frac{{32,4}}{{{x^2}}}}} = \frac{{54}}{{3,6x + \frac{{32,4}}{x}}}\)
Imax khi mẫu min
Ta có:
\(3,6{\rm{x}} + \frac{{32,4}}{x} \ge 2\sqrt {3,6{\rm{x}}.\frac{{32,4}}{x}} = 21,6\)
Dấu “=” xảy ra khi \(3,6{\rm{x}} = \frac{{32,4}}{x} \to x = 3\)
Khi đó : Imax = 2,5A
Khối lượng kẽm bám vào catốt của bình điện phân trong thời gian 1 giờ 4 phút 20 giây là:
\(m = \frac{1}{F}\frac{A}{n}It = \frac{1}{{96500}}\frac{{65}}{2}.2,5.(60.60 + 4.60 + 20) = 3,25g\)
Cho mạch điện như hình vẽ: Nguồn điện có suất điện động \(E = 12V\), điện trở trong r = \(1\Omega \), \({R_2} = 12\Omega \) và là bình điện phân đựng dung dịch \(AgN{O_3}\) với điện cực anôt bằng bạc, \({R_1} = 3\Omega \), \({R_3} = 6\Omega \). Cho biết bạc (Ag) có khối lượng mol là 108g/mol, hóa trị 1, hằng số Faraday F = 96500C/mol. Khối lượng bạc bám vào catot sau thời gian 16 phút 5 giây là
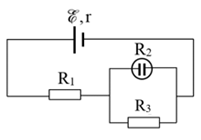
Cấu tạo mạch: \(\left( {{R_2}//{R_3}} \right)nt{R_1}\)
Ta có: \({R_{23}} = \dfrac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} = \dfrac{{12.6}}{{12 + 6}} = 4\,\,\left( \Omega \right)\)
\( \Rightarrow {R_N} = {R_1} + {R_{23}} = 3 + 4 = 7\,\,\left( \Omega \right)\)
Áp dụng định luật Ôm cho toàn mạch, ta có:
\(I = \dfrac{E}{{{R_N} + r}} = \dfrac{{12}}{{7 + 1}} = 1,5\,\,\left( A \right) = {I_1} = {I_{23}}\)
Ta có: \({U_{23}} = {I_{23}}.{R_{23}} = 1,5.4 = 6\,\,\left( V \right) = {U_2} = {U_3}\)
\( \Rightarrow {I_2} = \dfrac{{{U_2}}}{{{R_2}}} = \dfrac{6}{{12}} = 0,5\,\,\left( A \right)\)
Khối lượng bạc bám vào catot là:
\({m_{Ag}} = \dfrac{1}{F}.\dfrac{A}{n}.{I_2}t = \dfrac{1}{{96500}}.\dfrac{{108}}{1}.0,5.\left( {16.60 + 5} \right) = 0,54\,\,\left( g \right)\)
Một bình điện phân đựng dung dịch CuSO4 có anốt bằng đồng. Hiệu điện thế đặt vào hai cực là 6 V. Sau 16 phút 5 giây, lượng đồng bám vào cực âm là 0,48 g (Cho Cu có A = 64, n = 2). Điện trở của bình điện phân là
Cường độ dòng điện chạy qua bình điện phân là \(m = \frac{1}{F}.\frac{A}{n}.I.t = > I = \frac{{m.F.n}}{{A.t}} = \frac{{0,48.96494.2}}{{64.965}} = 1,5A\)
Điện trở của bình điện phân là \(R = \frac{\xi }{I} = \frac{6}{{1,5}} = 4\Omega \)
Một bình điện phân dung dịch CuSO4 có anốt làm bằng đồng, điện trở của bình điện phân R = 8(Ω), được mắc vào hai cực của bộ nguồn E = 9(V), điện trở trong r = 1(Ω). Cho ACu = 64(đvc), nCu=2. Khối lượng Cu bám vào ca tốt trong thời gian 5h có giá trị là:
Cường độ dòng điện chạy qua bình điện phân là \(I = {E \over {R + r}} = {9 \over {8 + 1}} = 1\left( A \right)\)
Khối lượng Cu bám vào ca tốt trong thời gian 5h là
\(m = {1 \over F}{A \over n}It = {1 \over {96500}}.{{64} \over 2}.1.5.3600 = 5,97g\)

