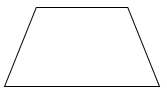
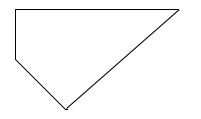
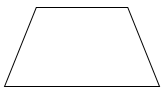
Trong các hình sau, hình nào là hình bình hành?
C.

C.

C.

Quan sát các hình đã cho ta thấy hình A là hình tròn; hình B là hình thang, hình D là tứ giác ; hình C có hai cặp cạnh đối diện song song và bằng nhau nên hình C là hình bình hành.
Vậy trong các hình đã cho, hình C là hình bình hành.
Hình dưới đây có bao nhiêu tứ giác ?

B. $3$ hình
B. $3$ hình
B. $3$ hình
Hình đã cho có các tứ giác là: hình $1$, hình $2$ và hình $1+2$.
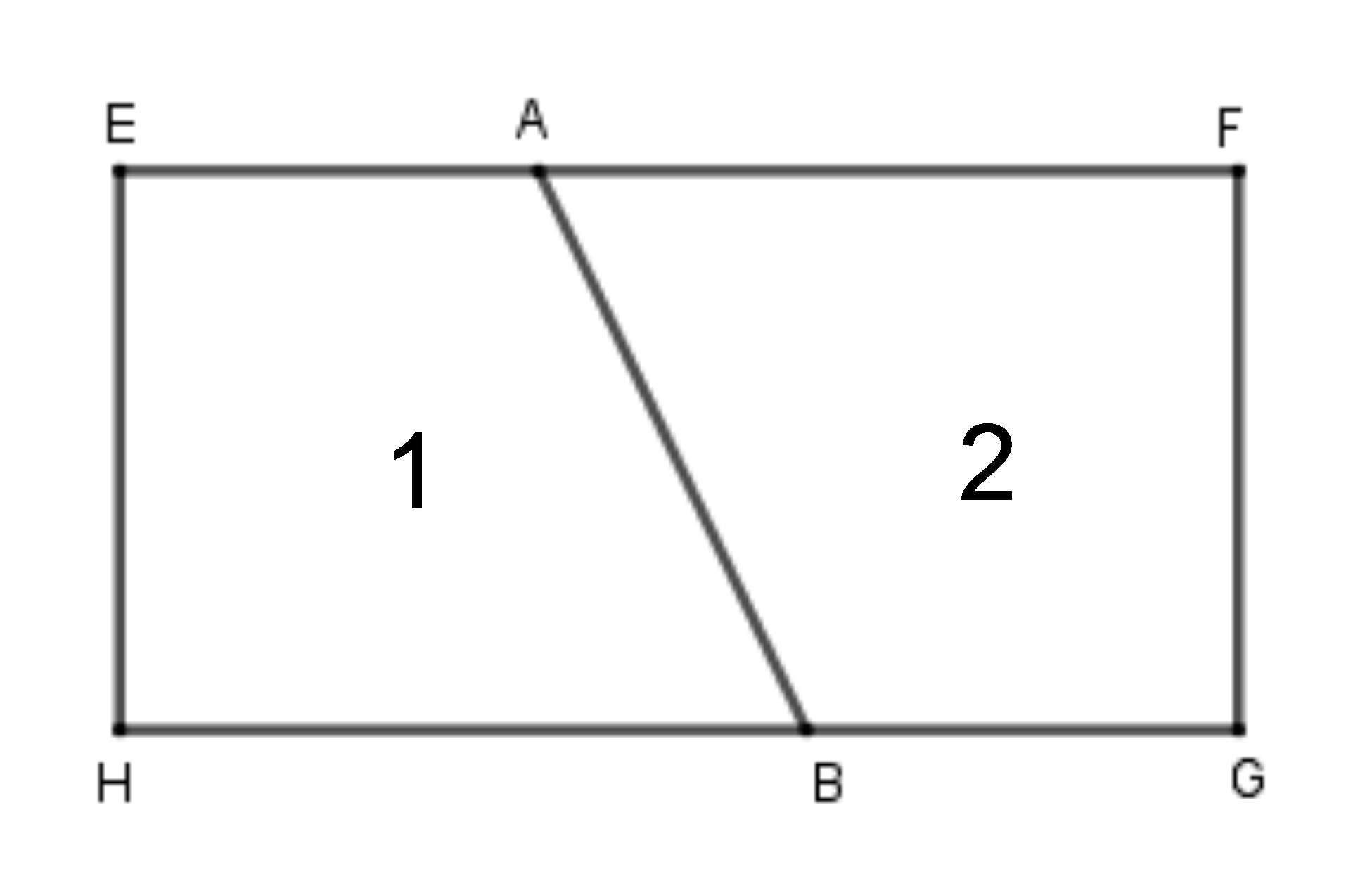
Hình đó có tất cả $3$ hình tứ giác.

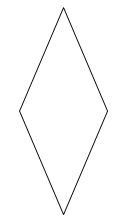
Trong các hình sau, hình nào là hình thoi?
B.
B.

B.

Quan sát các hình đã cho ta thấy hình A là hình thang, hình B là hình thoi, hình C là hình tròn, hình D là hình bình hành.
Vậy trong các hình đã cho, hình B là hình thoi.
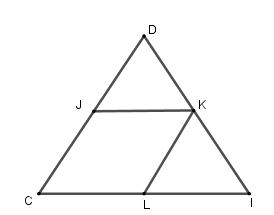
Hình trên có:
D. $3$ tam giác và $3$ tứ giác
D. $3$ tam giác và $3$ tứ giác
D. $3$ tam giác và $3$ tứ giác
Hình bên có các tam giác là: DJK; KLI và CDI.
Và có các hình tứ giác là: CJKL; CJKI; CDKL.
Đáp án cần chọn là D.
Cho hình vẽ như sau:
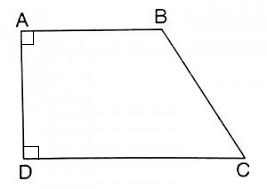
Cạnh AB song song với cạnh nào dưới đây?
B. DC
B. DC
B. DC
Quan sát hình vẽ ta thấy cạnh AB song song với cạnh DC.
Điền số thích hợp vào ô trống:

Hình chữ nhật MNPQ có
cặp cạnh vuông góc với nhau.
Hình chữ nhật MNPQ có
cặp cạnh vuông góc với nhau.
Trong hình chữ nhật MNPQ có:
MN vuông góc với MQ; MN vuông góc với NP;
PQ vuông góc với PN; PQ vuông góc với QM.
Vậy hình chữ nhật MNPQ có \(4\) cặp cạnh vuông góc với nhau.
Đáp án đúng điền vào ô trống là \(4\).
Cho hình chữ nhật và hình vuông có kích thước như hình vẽ:
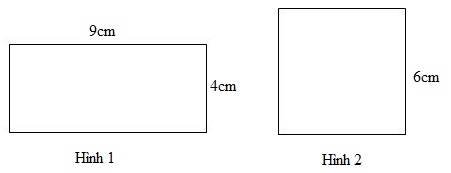
a) Chu vi hình \(1\) bằng chu vi hình \(2\).
b) Diện tích hình \(1\) bằng diện tích hình \(2\).
c) Diện tích hình \(2\) lớn hơn diện tích hình \(1\).
d) Chu vi hình \(1\) lớn hơn chu vi hình \(2\).
a) Chu vi hình \(1\) bằng chu vi hình \(2\).
b) Diện tích hình \(1\) bằng diện tích hình \(2\).
c) Diện tích hình \(2\) lớn hơn diện tích hình \(1\).
d) Chu vi hình \(1\) lớn hơn chu vi hình \(2\).
Chu vi hình \(1\) là: \((9 + 4) \times 2 = 26\,\,(cm)\)
Diện tích hình \(1\) là: \(9 \times 4 = 36\,\,(c{m^2})\)
Chu vi hình \(2\) là: \(6 \times 4 = 24\,\,(cm)\)
Diện tích hình \(2\) là: \(6 \times 6 = 36\,\,(c{m^2})\)
Ta có \(26cm > 24cm\) nên chu vi hình \(1\) lớn hơn chu vi hình \(2\).
\(36c{m^2} = 36c{m^2}\) nên diện tích hình \(1\) bằng diện tích hình \(2\).
Vậy các kết luận đúng là b và d; kết luận sai là a và c.

Hình tam giác ABC có chu vi là $48m$. Độ dài cạnh $AB=15m$, $BC=400cm$.
Độ dài cạnh AC là
$m$.
Độ dài cạnh AC là
$m$.
Đổi: $400cm=4m$
Độ dài cạnh AC là:
$48-15-4=29\left( m \right)$
Đáp số: $29m$.
Cần điền vào chỗ trống là $29$.

Một tam giác có chu vi tam giác giảm đi $6m$ thì còn lại là $21m$. Hỏi độ dài mỗi cạnh của tam giác đó bằng bao nhiêu biết rằng độ dài ba cạnh của tam giác đó bằng nhau?
D. $9m$
D. $9m$
D. $9m$
Chu vi của hình tam giác lúc ban đầu là:
$21+6=27\left( m \right)$
Độ dài mỗi cạnh của tam giác là:
$27:3=9\left( m \right)$
Đáp số: $9m$.

Diện tích hình thoi có độ dài hai đường chéo \(9cm\) và \(16cm\) là:
C. \(72c{m^2}\)
C. \(72c{m^2}\)
C. \(72c{m^2}\)
Diện tích hình thoi đó là:
\(\dfrac{{9 \times 16}}{2} = 72\left( {c{m^2}} \right)\)
Đáp số: \(72c{m^2}\)
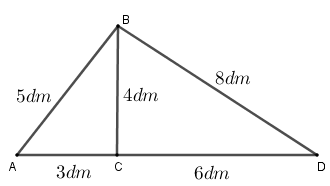
Tổng chu vi của hai tam giác ABC và BCD là:
A. $30dm$
A. $30dm$
A. $30dm$
Chu vi tam giác ABC là:
$3+4+5=12\left( dm \right)$
Chu vi tam giác BCD là:
$4+6+8=18\left( dm \right)$
Tổng chu vi của hai tam giác ABC và BCD là:
$12+18=30\left( dm \right)$
Đáp số:\(30dm\).
.jpg)
Điền số thích hợp ô trống:
Hình bình hành có cạnh đáy dài \(27cm\), chiều cao \(14cm\).
Diện tích hình bình hành đó là
\(\,c{m^2}\).
Hình bình hành có cạnh đáy dài \(27cm\), chiều cao \(14cm\).
Diện tích hình bình hành đó là
\(\,c{m^2}\).
Diện tích hình bình hành đó là:
\(27 \times 14 = 378\left( {c{m^2}} \right)\)
Đáp số: \(378c{m^2}\)
Vậy đáp án đúng điền vào ô trống là \(378\).
.jpg)
Một hình bình hành có cạnh đáy dài \(\dfrac{4}{5}m\), chiều cao bằng một nửa cạnh đáy. Diện tích hình bình hành đó là:
C. \(\dfrac{8}{{25}}{m^2}\)
C. \(\dfrac{8}{{25}}{m^2}\)
C. \(\dfrac{8}{{25}}{m^2}\)
Chiều cao của hình bình hành đó là:
\(\dfrac{4}{5}:2 = \dfrac{2}{5}\,\,(m)\)
Diện tích hình bình hành đó là:
\(\dfrac{4}{5} \times \dfrac{2}{5} = \dfrac{8}{{25}}\,\,({m^2})\)
Đáp số: \(\dfrac{8}{{25}}{m^2}\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hình thoi ABCD có độ dài đường chéo AC là \(40cm\), độ dài đường chéo BD bằng \(\dfrac{3}{5}\) độ dài đường chéo AC. Hình chữ nhật GHIK có chiều rộng là \(15cm\) và diện tích bằng diện tích hình thoi ABCD.
Vậy chu vi hình chữ nhật GHIK là
\(cm\).
Hình thoi ABCD có độ dài đường chéo AC là \(40cm\), độ dài đường chéo BD bằng \(\dfrac{3}{5}\) độ dài đường chéo AC. Hình chữ nhật GHIK có chiều rộng là \(15cm\) và diện tích bằng diện tích hình thoi ABCD.
Vậy chu vi hình chữ nhật GHIK là
\(cm\).
Độ dài đường chéo BD là:
\(40 \times \dfrac{3}{5} = 24\,\,(cm)\)
Diện tích hình thoi ABCD là:
\(40 \times 24\,:2 = 480\,\,(c{m^2})\)
Vì hình chữ nhật GHIK có diện tích bằng diện tích hình thoi ABCD nên diện tích hình chữ nhật GHIK là \(480c{m^2}\).
Chiều dài hình chữ nhật là:
\(480:15 = 32\,\,(cm)\)
Chu vi hình chữ nhật là:
\((32 + 15) \times 2 = 94\,\,(cm)\)
Đáp số: \(94cm\).
Vậy đáp án đúng điền vào ô trống là \(94\).

Để lát nền một phòng học hình chữ nhật người ta dùng loại gạch men hình vuông có cạnh \(30cm\). Hỏi cần bao nhiêu viên gạch để lát kín nền phòng học đó, biết rằng nền phòng học có chiều rộng \(6m\) và chiều dài \(12m\) và phần mạch vữa không đáng kể?
B. \(800\) viên gạch
B. \(800\) viên gạch
B. \(800\) viên gạch
Diện tích một viên gạch là:
\(30 \times 30 = 900\,\,(c{m^2})\)
Diện tích căn phòng đó là:
\(\begin{array}{l}12 \times 6 = 72\,\,({m^2})\\72{m^2} = 720000c{m^2}\end{array}\)
Để lát kín nền căn phòng đó người ta cần dùng số viên gạch là:
\(720000:900 = 800\) (viên gạch)
Đáp số: \(800\) viên gạch.
Điền số thích hợp vào ô trống:

Biết hình bình hành ABCD có $AB = 56cm$ và $BC = 24cm$, đường cao $AH = 15cm$.
Vậy độ dài đường cao AK tương ứng với cạnh BC là
$cm$.
Biết hình bình hành ABCD có $AB = 56cm$ và $BC = 24cm$, đường cao $AH = 15cm$.
Vậy độ dài đường cao AK tương ứng với cạnh BC là
$cm$.
Vì ABCD là hình bình hành nên $AB = CD = 56cm$.
Diện tích hình bình hành đó là:
$56 \times 15 = 840\,\,\left( {c{m^2}} \right)$
Độ dài đường cao AK là:
$840:24 = 35\,\,\left( {cm} \right)$
Đáp số: \(35cm\).
Vậy đáp án đúng điền vào ô trống là \(35\).
Tính diên tích mảnh đất có kích thước như hình vẽ như bên dưới:

D. \(560{m^2}\)
D. \(560{m^2}\)
D. \(560{m^2}\)
Chia mảnh đất đã cho thành \(3\) mảnh đất hình chữ nhật như sau:
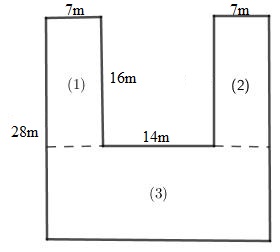
Gọi \(S\) là diện tích mảnh đất ban đầu, \({S_1},\,\,{S_2},\,\,{S_3}\) lần lượt là diện tích các mảnh đất \((1),\,(2),\,(3)\) . Khi đó \(S = {S_1} + {S_2} + {S_3}\).
Diện tích mảnh đất thứ nhất là:
\(16 \times 7 = 112\,\,({m^2})\)
Diện tích mảnh đất thứ hai là:
\(16 \times 7 = 112\,\,({m^2})\)
Chiều rộng của mảnh đất thứ ba là:
\(28 - 16 = 12\,\,(m)\)
Chiều dài của mảnh đất thứ ba là:
\(7 + 14 + 7 = 28\,\,(m)\)
Diện tích mảnh đất thứ ba là:
$28 \times 12 = 336\,\,({m^2})$
Diện tích mảnh đất ban đầu là:
$112 + 112 + 336 = 560\,\,({m^2})$
Đáp số: \(560{m^2}\)