
Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số. Đúng hay sai?
A. Đúng
A. Đúng
A. Đúng
Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Vậy phát biểu đã cho là đúng.

Phép nhân phân số có những tính chất nào dưới đây?
D. Tất cả các đáp án trên đều đúng
D. Tất cả các đáp án trên đều đúng
D. Tất cả các đáp án trên đều đúng
Phép nhân phân số có các tính chất:
+) Tính chất giao hoán : Khi đổi chỗ các phân số trong một tích thì tích của chúng không thay đổi.
a×b=b×a
+) Tính chất kết hợp: Khi nhân một tích hai phân số với phân số thứ ba, ta có thể nhân phân số thứ nhất với tích của hai phân số còn lại.
(a×b)×c=a×(b×c)
+ Tính chất phân phối: Khi nhân một tổng hai phân số với phân số thứ ba, ta có thể nhân lần lượt từng phân số của tổng với phân số thứ ba rồi cộng các kết quả đó lại với nhau.
(a+b)×c=a×c+b×c
+ Nhân với số 1: Phân số nào nhân với 1 cũng bằng chính phân số đó.
a×1=1×a=a
+ Nhân với số 0: Phân số nào nhân với 0 cũng bằng 0.
a×0=0×a=0
Vậy tất cả các đáp án A, B, C đều đúng.

Thực hiện tính:
Ta có: 35×47=3×45×7=1235
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là 12;35.

Điền số thích hợp vào chỗ chấm:
35×47=......
B. 12;35
B. 12;35
B. 12;35
Ta có: 35×47=3×45×7=1235
Vậy đáp án đúng điền vào chỗ chấm lần lượt từ trên xuống dưới là 12;35.
.jpg)
Tính rồi rút gọn : 58×415
C. 16
C. 16
C. 16
Ta có:
58×415=5×48×15=5×44×2×5×3=16
Vậy đáp án đúng là 16.

Rút gọn rồi tính: 2530×68
B. 58
B. 58
B. 58
Ta có:
2530×68=56×34=5×36×4=5×33×2×4=58
Vậy đáp án đúng là 58.

Thực hiện tính:
Ta có:
67×8=67×81=6×87×1=487
Hoặc ta có thể viết gọn như sau: 67×8=6×87=487
Vậy đáp án đúng điền vào chỗ chấm lần lượt từ trên xuống dưới là 48;7.

Thực hiện tính:
Phân số nào nhân với 1 cũng bằng chính phân số đó.
Do đó, ta có: 79×1=79
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là 7;9.

Điền số thích hợp vào chỗ chấm :
67×8=......
A. 48;7
A. 48;7
A. 48;7
Ta có:
67×8=67×81=6×87×1=487
Hoặc ta có thể viết gọn như sau: 67×8=6×87=487
Vậy đáp án đúng điền vào chỗ chấm lần lượt từ trên xuống dưới là 48;7.

Điền số thích hợp vào chỗ chấm :
79×1=......
A. 7;9.
A. 7;9.
A. 7;9.
Phân số nào nhân với 1 cũng bằng chính phân số đó.
Do đó, ta có: 79×1=79
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là 7;9.

Tìm x, biết: x:712=12−27
A. x=18
A. x=18
A. x=18
Ta có:
x:712=12−27x:712=314x=314×712x=18
Vậy x=18.

Tính: 6×(58+34)
D. 334
D. 334
D. 334
Ta có:
6×(58+34)=6×(58+68)=6×118=6×118=3×2×114×2=334
Vậy đáp án đúng là 334.

Điền dấu thích hợp vào chỗ chấm:
Một hình vuông có cạnh 58m. Vậy chu vi hình vuông đó là... ; diện tích hình vuông đó là....
A. 25;64
A. 25;64
A. 25;64
Chu vi hình vuông đó là:
58×4=52(m)
Diện tích hình vuông đó là:
58×58=2564(m2)
Đáp số: Chu vi: 52m ; Diện tích: 2564m2
Vậy đáp án đúng điền vào ô trống thứ nhất lần lượt từ trên xuống dưới là 5;2 ; đáp án điền ô trống thứ hai lần lượt từ trên xuống dưới là 25;64.

Kết quả của phép tính: 23×45×94 là:
B. 65
B. 65
B. 65
Ta có:
23×45×94=2×4×93×5×4=2×4×3×33×5×4=65
Vậy đáp án đúng là 65.

Chọn dấu thích hợp điền vào ô trống:
34×815+13⋅⋅⋅2−25×3
A. <
A. <
A. <
Ta có:
+) 34×815+13=25+13=1115 ;
+) 2−25×3=2−65=45=1215
Mà 1115<1215, hay 1115<45.
Do đó 34×815+13<2−25×3.
Vậy dấu thích hợp điền vào ô trống là <.
.gif)
Điền số thích hợp vào ô trống:
Tính bằng cách thuận tiện
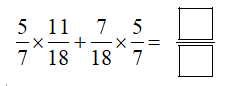
C. 57
C. 57
C. 57
57×1118+718×57=57×(1118+718)=57×818=57×1=57

Điền số thích hợp vào ô trống (điền phân số dạng tối giản)
Một hình vuông có cạnh là 58m.
Chu vi hình vuông đó là:
58×4=52(m)
Diện tích hình vuông đó là:
58×58=2564(m2)
Đáp số: Chu vi: 52m ;
Diện tích: 2564m2.
Vậy đáp án đúng điền vào ô trống thứ nhất lần lượt từ trên xuống dưới là 5;2 ; đáp án điền ô trống thứ hai lần lượt từ trên xuống dưới là 25;64.

Tính bằng cách thuận tiện:
57×1118+718×57=57×(1118+718)=57×1818=57×1=57

Bác Lan trồng cà chua trên một mảnh vườn hình chữ nhật có chiều rộng là 352m, chiều dài gấp 4 lần chiều rộng. Biết rằng cứ 1m2 thì thu được 3kg cà chua, vậy trên cả mảnh vườn đó bác Lan thu được số ki-lô-gam cà chua là:
C. 3675kg
C. 3675kg
C. 3675kg
Chiều dài mảnh vườn đó là:
352×4=70(m)
Diện tích mảnh vườn đó là:
352×70=1225(m2)
Trên cả mảnh vườn đó bác Lan thu được số ki-lô-gam cà chua là:
1225×3=3675(kg)
Đáp số: 3675kg.

