Dấu hiệu chia hết cho 2

Các số có chữ số tận cùng là $0;\,\,2;\,\,4;\,\,6;\,\,\,8$ thì chia hết cho $2$.

Vậy khẳng định đã cho là đúng.

Số chia hết cho $2$ là số chẵn. Số không chia hết cho $2$ là số lẻ.

Vậy khẳng định “Số không chia hết cho $2$ là số chẵn” là sai.

Số $1235$ có chữ số tận cùng là $5$ nên $1235$ không chia hết cho $2$.

Số $1331$ có chữ số tận cùng là $1$ nên $1331$ không chia hết cho $2$.

Số $2469$ có chữ số tận cùng là $9$ nên $2469$ không chia hết cho $2$.

Số $1998$ có chữ số tận cùng là $8$ nên $1998$ chia hết cho $2$.

Vậy trong các số đã cho, số chia hết cho $2$ là $1998$.

Dãy A có số $1247$ có chữ số tận cùng là $7$ nên $1247$ không chia hết cho $2$.

Dãy B  gồm các số chữ số tận cùng là $0;\,\,2;\,\,4;\,\,6;\,\,8$ nên chia hết cho $2$.

Dãy C gồm các số chữ số tận cùng là $1;\,\,3;\,\,5;\,\,7;\,\,9$ nên không chia hết cho $2$.

Dãy D có số $6035$ có chữ số tận cùng là $5$ nên $6035$ không chia hết cho $2$.

Vậy dãy gồm các số chia hết cho 2 là $36\,;\,\,148\,;\,\,8750\,;\,\,17952\,;\,\,3344$.

Những số có chữ số tận cùng là $1;\,\,3;\,\,5;\,\,7;\,\,9$ thì  không chia hết cho $2$.

Do đó trong các số đã cho, các số không chia hết cho $2$ là $35\,;\,\,99\,;\,\,237\,;\,\,2461$ .

Vậy có $4$ số không chia hết cho $2$.

Nếu $a = 1$ thì số $6131$ có chữ số tận cùng là $1$ nên không chia hết cho $2$.

Nếu $a = 3$ thì số $6133$ có chữ số tận cùng là $3$ nên không chia hết cho $2$.

Nếu $a = 7$ thì số $6137$ có chữ số tận cùng là $7$ nên không chia hết cho $2$.

Nếu $a = 8$ thì số $6138$ có chữ số tận cùng là $8$ nên chia hết cho $2$.
Vậy đáp án đúng là  $a = 8$.

Ta có: Các số có chữ số tận cùng là $1;\,\,3;\,\,5;\,\,7;\,\,9$  thì không chia hết cho $2$.

Do đó để số $\overline {493b}$ không chia hết cho $2$ thì $b = 1\,;\,\,3\,;\,\,5\,;\,\,7\,;\,\,9$.

Từ ba chữ số $1;\,\,6;\,\,9$ viết được các số có hai chữ số khác nhau là $16\,;\,\,19\,;\,\,61\,;\,\,69\,;\,\,91\,;\,\,96$.

Các số $\,19;\,\,69;\,\,\,61\,;\,\,91$ có chữ số tận cùng là $1$ và $9$ nên không chia hết cho $2$.

Vậy từ ba chữ số $1;\,\,6;\,\,9$ ta viết được các số có hai chữ số khác nhau và không chia hết cho 2 là $19\,;\,\,69\,;\,\,61\,;\,\,91$.

Tổng các chữ số của $\overline {1596y}$ là:   $1 + 5 + 9 + 6 + y = 21 + y$.

Vì tổng các chữ số lớn hơn $27$ nên $y$ chỉ có thể là $7\, ;\,\,8$  hoặc $9$.

Nếu $y = 7$ thì số $15967$ có chữ số tận cùng là $7$ nên không chia hết cho $2$.

Nếu $y = 8$ thì số $15968$ có chữ số tận cùng là $8$ nên chia hết cho $2$.

Nếu $y = 9$ thì số $15969$ có chữ số tận cùng là $9$ nên không chia hết cho $2$.

Vậy để số $\overline {1596y}$ chia hết cho 2 và tổng các chữ số lớn hơn $27$ thì $y = 8$.

Ta có:

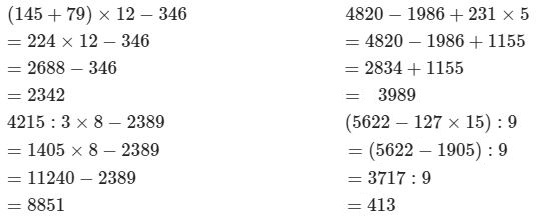
Trong các số trên chỉ có số $2342$ có chữ số tận cùng là $2$ nên $2342$ chia hết cho $2$, ngoài ra không còn số nào chia hết cho $2$.

Do đó giá trị biểu thức $(145 + 79) \times 12 - 346$ là số chia hết cho $2$.

$\begin{array}{l}550 + 2 = 552\\552 + 2 = 554\end{array}$   

Suy ra quy luật là: Từ số hạng thứ hai trở đi bằng số hạng liền trước cộng thêm $2$ đơn vị.

Số thứ tư là:                $554 + 2 = 556$.

Số thứ năm là:             $556 + 2 = 558$

Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là $556\,;\,\,558$.

Số cần điền lớn hơn $500$  và nhỏ hơn $504$ nên số cần điền chỉ có thể là $501\,;\,\,502\,;\,\,503$.
Trong $3$ số đó chỉ có số $502$ chia hết cho $2$ vì có chữ số tận cùng là $2$.
Vậy đáp án đúng điền vào ô trống là $502$.

Vì tuổi của mẹ Lan ít hơn $44$ tuổi nhưng nhiều hơn $40$ tuổi nên tuổi của mẹ Lan chỉ có thể là $41,{\rm{ 42}},{\rm{ 43}}$ .

Nếu đem số tuổi của mẹ Lan chia cho $2$ thì không dư nên tuổi của mẹ Lan phải là số chia hết cho $2$.

Trong ba số $41,{\rm{ 42}},{\rm{ 43}}$, chỉ có số $42$ chia hết cho $2$ vì có chữ số tận cùng là $2$.

Do đó tuổi của mẹ Lan là $42$ tuổi.

Vậy đáp án đúng điền vào ô trống là $42$.

Để lập được số chia hết cho $2$ thì các số đó phải có chữ số tận cùng là $0;{\rm{ }}2;{\rm{ }}4;{\rm{ }}6;{\rm{ }}8$.

Do đó các số có chia hết cho $2$ được lập từ bốn chữ số $0,{\rm{ 4}},{\rm{ 5,}}\,7$ phải có chữ số tận cùng là $0$ hoặc $4$.

Từ bốn chữ số $0,{\rm{ 4}},{\rm{ 5,}}\,7$ ta viết được các số có ba chữ số khác nhau và chia hết cho $2$ là:

$450\,;\,\,470\,;\,540\,;\,\,570;\,\,740\,;\,\,750;\,\,\,504\,;\,\,574\,;\,\,704\,;754.$

Có $10$ số có ba chữ số khác nhau và chia hết cho $2$.
Vậy đáp án đúng điền vào ô trống là $10$.