
D. Tất cả các đáp án trên đều đúng.
D. Tất cả các đáp án trên đều đúng.
D. Tất cả các đáp án trên đều đúng.
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.
- Phân số có tử số bé hơn mẫu số thì bé hơn 1.
Vậy tất cả các đáp án trên đều đúng.

Hoa nói: “Trong hai phân số có cùng mẫu số, phân số nào có tử số lớn hơn thì bé hơn”. Theo con, Hoa nói đúng hay sai?
B. Sai
B. Sai
B. Sai
Trong hai phân số có cùng mẫu số:
+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.
+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Vậy Hoa đã nói sai.
Cho hình vẽ như bên dưới:
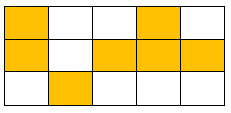
Phân số chỉ phần tô màu trong hình vẽ trên là:
A. 715
A. 715
A. 715
Quan sát hình vẽ ta thấy có tất cả 15 ô vuông, trong đó có 7 ô vuông được tô màu.
Vậy phân số chỉ số ô vuông đã tô màu trong hình là 715.

Thương của phép chia a:(b+c) được viết dưới dạng phân số là:
D. ab+c
D. ab+c
D. ab+c
Mọi phép chia đều có thể viết dưới dạng phân số, trong đó tử số là số bị chia và mẫu số là số chia
Phép chia a:(b+c) có a là số bị chia và b+c là số chia.
Ta có: a:(b+c)=ab+c
Vậy thương của phép chia a:(b+c) được viết dưới dạng phân số là ab+c.

Ta có: 47=4×37×3=1221.

Điền số thích hợp vào chỗ chấm:
47=4×37×...=......
A. 12;3;21
A. 12;3;21
A. 12;3;21
Ta có:
47=4×37×3=1221
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải, từ trên xuống dưới là 12;3;21.

Từ các số 5;9 ta có thể lập được bao nhiêu phân số có tử số và mẫu số là một trong các số đó (trong đó tử số phải khác mẫu số)?
B. 2 phân số
B. 2 phân số
B. 2 phân số
Từ các số 5;9 ta có thể lập được các phân số có tử số và mẫu số là một trong các số đã cho đó là:
55;59;95;99
Ta thấy trong các phân số vừa lập có 2 phân số có tử số khác mẫu số đó là: 59;95.
Vậy từ các số 5;9 ta có thể lập được 2 phân số có tử số và mẫu số là một trong các số đó (trong đó tử số phải khác mẫu số).

Mẹ đi chợ mua về 2 chục quả cam, mẹ đem biếu bà hết 14 số cam đó, biếu bác Lan 4 quả cam.
Đổi : 2 chục quả cam =20 quả cam.
Mẹ đã biếu bà số quả cam là:
20:4=5 (quả cam)
Số quả cam mẹ đã biếu bà và bác Lan là
5+4=9 (quả cam)
Số quả cam còn lại là:
20−9=11 (quả cam)
Vậy phân số chỉ số quả cam còn lại là 1120.
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là 11;20.
.jpg)
Điền số thích hợp vào chỗ chấm:
Mẹ đi chợ mua về 2 chục quả cam, mẹ đem biếu bà hết 14 số cam đó, biếu bác Lan 4 quả cam. Vậy phân số chỉ số cam còn lại là ...... .
A. 11;20
A. 11;20
A. 11;20
Đổi : 2 chục quả cam =20 quả cam.
Mẹ đã biếu bà số quả cam là:
20:4=5 (quả cam)
Số quả cam mẹ đã biếu bà và bác Lan là
5+4=9 (quả cam)
Số quả cam còn lại là:
20−9=11 (quả cam)
Vậy phân số chỉ số quả cam còn lại là: 1120.
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là 11;20.
.jpg)
Phân số nào sau đây khi rút gọn được phân số tối giản là 58 ?
B. 4572
B. 4572
B. 4572
Phân số 821 là phân số tối giản nên không thể rút gọn được nữa.
Ta có:
75115=75:5115:5=1523;4572=45:972:9=58;
3545=35:545:5=78.
Vậy khi rút gọn phân số 4572 ta được phân số tối giản là 58.

Tìm phân số ab, biết phân số ab là phân số tối giản sau khi rút gọn phân số 105135.
C. ab=79
C. ab=79
C. ab=79
Rút gọn phân số 105135 ta có:
105135=105:5135:5=2127=21:327:3=79
Ta thấy 7 và 9 không cùng chia hết cho số tự nhiên nào lớn hơn 1 nên 79 là phân số tối giản.
Vậy ab=79.

Quy đồng mẫu số phân số 78 và 56 ta được hai phân số lần lượt là:
Chọn mẫu số chung là 24.
Vì 24:8=3 nên ta quy đồng mẫu số phân số 78 như sau:
78=7×38×3=2124
Vì 24:6=4 nên ta quy đồng mẫu số phân số 56 như sau:
56=5×46×4=2024
Vậy quy đồng mẫu số phân số 78 và 56 ta được hai phân số lần lượt là 2124 và 2024.

Điền số thích hợp vào chỗ chấm:
Quy đồng mẫu số phân số 78 và 56 ta được hai phân số lần lượt là 2124 và ......
A. 20;24
A. 20;24
A. 20;24
Chọn mẫu số chung là 24.
Vì 24:6=4 nên ta quy đồng mẫu số phân số 56 như sau:
56=5×46×4=2024
Vậy quy đồng mẫu số phân số 78 và 56 ta được hai phân số lần lượt là 2124 và 2024.
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là 20;24.

Ngày thứ nhất An uống hết 23 lít sữa. Ngày thứ hai An uống hết 34 lít sữa. Hỏi trong hai ngày đó, ngày nào An uống nhiều sữa hơn?
B. Ngày thứ hai
B. Ngày thứ hai
B. Ngày thứ hai
Để biết ngày nào An uống nhiều sữa hơn ta sẽ so sánh hai phân số 23 và 34.
Quy đồng mẫu số hai phân số ta có:
23=2×43×4=812;
34=3×34×3=912
Vì 8<9 nên 812<912.
Do đó: 23<34.
Vậy ngày thứ hai An uống nhiều sữa hơn.

Điền số thích hợp vào ô trống:
Với ba số tự nhiên 4;7 và 9 ta viết được
phân số nhỏ hơn 1.
Với ba số tự nhiên 4;7 và 9 ta viết được
phân số nhỏ hơn 1.
Các phân số nhỏ hơn 1 là các phân số có tử số nhỏ hơn mẫu số.
Trong các số đã cho ta thấy: 4<7<9.
Vậy từ các số đã cho ta có thể lập được các phân số có tử số nhỏ hơn mẫu số như sau:
47;49;79
Vậy với ba số tự nhiên 4;7 và 9 ta viết được 3 phân số nhỏ hơn 1.
Đáp án đúng điền vào ô trống là 3.

Chọn dấu thích hợp để điền vào chỗ chấm:
11111112⋅⋅⋅20172019
A. >
A. >
A. >
Phần bù của 11111112 là 11112.
Phần bù của 20172019 là 22019.
Ta có: 11112=22224
Vì 2224>2019 nên 22224<22019, hay 11112<22019.
Do đó 11111112>20172019.

Có bao nhiêu phân số bằng phân số 1218 sao cho mẫu số nhỏ hơn 30?
D. 8 phân số
D. 8 phân số
D. 8 phân số
Vì phân số đã cho có mẫu số là 18 và 18×2=36,(36>30)(không thoả mãn điều kiện mẫu số nhỏ hơn 30) nên ta sẽ không nhân cả tử số và mẫu số của phân số 1218 với cùng số tự nhiên nào lớn hơn 1.
Rút gọn phân số 1218 ta có: 1218=12:618:6=23.
Ta sẽ tìm các phân số bằng phân số 23 và có mẫu số nhỏ hơn 30.
23=2×23×2=46;23=2×33×3=6923=2×43×4=812;23=2×53×5=101523=2×63×6=1218;23=2×73×7=142123=2×83×8=1624;23=2×93×9=1827⋅
Vậy có 8 phân số bằng với phân số 1218 mà mẫu số nhỏ hơn 30 là:
23;46;69;812;1015;1421;1624;1827⋅

