Một hạt electron với vận tốc ban đầu bằng \(0\), được gia tốc qua một hiệu điện thế \(400\,\,\left( V \right)\). Tiếp đó, nó được dẫn vào một miền từ trường với véc-tơ cảm ứng từ vuông góc với véc-tơ vận tốc của electron. Quỹ đạo của electron là một đường tròn bán kính \(R = 7\,\,\left( {cm} \right)\). Độ lớn cảm ứng từ là
Áp dụng định lí biến thiên động năng cho electron, ta có:
\({W_{ds}} - {W_{dt}} = A \Rightarrow \frac{1}{2}m{v^2} - 0 = \left| e \right|.U \Rightarrow v = \sqrt {\frac{{2\left| e \right|.U}}{m}} \)
Bán kính chuyển động của electron tỏng từ trường là:
\(\begin{array}{l}R = \frac{{mv}}{{\left| e \right|B}} = \frac{{m.\sqrt {\frac{{2\left| e \right|U}}{m}} }}{{\left| e \right|.B}} = \frac{1}{B}.\sqrt {\frac{{2m.U}}{{\left| e \right|}}} \Rightarrow B = \frac{1}{R}.\sqrt {\frac{{2m.U}}{{\left| e \right|}}} \\ \Rightarrow B = \frac{1}{{{{7.10}^{ - 2}}}}.\sqrt {\frac{{2.9,{{1.10}^{ - 31}}.400}}{{\left| { - 1,{{6.10}^{ - 19}}} \right|}}} \approx 0,{96.10^{ - 3}}\,\,\left( T \right)\end{array}\)
Một proton chuyển động thẳng đều trong miền có cả từ trường đều và điện trường đều. Vectơ vận tốc của hạt và hướng đường sức điện trường như hình vẽ. \(E = 8000V/m;v = {2.10^6}m/s\). Xác định hướng và độ lớn \(B\):
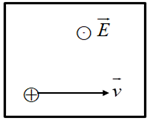
Proton chuyển động thẳng đều trong miền có cả từ trường đều và điện trường đều nên:
\(\overrightarrow {{F_d}} + \overrightarrow {{F_L}} = \overrightarrow 0 \Leftrightarrow \overrightarrow {{F_d}} = - \overrightarrow {{F_L}} \)
Lực điện: \(\overrightarrow {{F_d}} = q\overrightarrow E \) có hướng từ trong ra ngoài nên lực Lorenxo có hướng từ ngoài vào trong.
Áp dụng quy tắc bàn tay trái xác định được chiều của \(\overrightarrow B \) hướng từ trên xuống.
Với độ lớn: \({{F_d} = {F_L} \Leftrightarrow qE = qB.v.\sin \alpha }\)
\({ \Rightarrow B = \dfrac{E}{{v.\sin \alpha }} = \dfrac{{8000}}{{{{2.10}^6}.\sin 90}} = 0,004T}\)

