Bài tập phân tích dữ kiện, số liệu

Câu trả lời đúng là nó là một mối quan hệ tích cực, tuyến tính.

Như chúng ta có thể thấy trong phương trình, F tỉ lệ thuận với m không có số mũ liên quan. Điều này có nghĩa là nếu chúng ta tăng gấp đôi khối lượng thì lực cũng tăng lên gấp đôi.

- Trước tiên, chúng ta bỏ qua các biến vì chúng là thông tin không cần thiết.

Ta có: \({F_T} = \frac{{m{v^2}}}{R}\)

Giảm một nửa vận tốc => \(v' = \frac{v}{2}\)

Tăng gấp đôi khối lượng => m’ = 2m

Bán kính R giữ nguyên

Suy ra: \(F{'_T} = \frac{{2m{{\left( {\frac{v}{2}} \right)}^2}}}{R} = \frac{1}{2}.\frac{{m{v^2}}}{R} = \frac{{{F_T}}}{2} = \frac{{20}}{2} = 10N\)

+ Năng lượng tàu sử dụng trong 1 ngày:

\(\text{W}=P.t={{16.10}^{6}}.86400={{1,3824.10}^{12}}J\)

+ Do hiệu suất của lò là 30% nên năng lượng của mỗi phân hạch cung cấp là:

\(\Delta \text{W}=200.0,3=60MeV={{9,6.10}^{-12}}J\)

+ Số phân hạch cần xảy ra để có năng lượng W là:

\(N=\frac{\text{W}}{\Delta \text{W}}={{1,44.10}^{23}}\)

+ Cứ một phân hạch cần 1 hạt U²³⁵ → số hạt U²³⁵ dùng trong 1 ngày là:

\({{N}_{U}}~=N={{1,44.10}^{23}}~\,\left( hat \right)\)

+ Khối lượng U cần dùng trong 1 ngày:

\({{N}_{U}}=\frac{{{m}_{U}}}{A}.{{N}_{A}}\Rightarrow {{m}_{U}}=\frac{{{N}_{U}}.A}{{{N}_{A}}}=\frac{{{1,44.10}^{23}}.235}{{{6,02.10}^{23}}}=56,2126g\)

+ Nhiên liệu dùng trong lò là U làm giàu đến 12,5% (tính theo khối lượng)

→ Khối lượng nhiên liệu cần dùng trong  1 ngày:

\({{m}_{nl}}=\frac{{{m}_{U}}}{12,5%}=449,7g\)

+ Khối lượng nhiên liệu cần dùng trong 3 tháng là:

\(m=449,7.90=40,47kg\)

+ Năng lượng hạt nhân của lò phản ứng cung cấp cho tàu ngầm vận hành trong một ngày:

\(W=P.t={{400.10}^{6}}.86400={{3,456.10}^{13}}J\)

+ Do hiệu suất của lò đạt 25% nên năng lượng của mỗi phân hạch cung cấp là:

\(\Delta \text{W}=200.0,25=50MeV={{8.10}^{-12}}J\)

+ Số phân hạch cần xảy ra để có năng lượng W là:

\(N=\frac{\text{W}}{\Delta \text{W}}={{4,32.10}^{24}}\)

 + Cứ một phân hạch cần 1 hạt U²³⁵ → số hạt U²³⁵ dùng trong 1 ngày là: N = 4,32.10²⁴ hạt

+ Lại có:

\(N=\frac{m}{A}.{{N}_{A}}\Rightarrow m=\frac{N.A}{{{N}_{A}}}=\frac{{{4,23.10}^{24}}.235}{{{6,02.10}^{23}}}\approx 1686,4g=1,69kg\)

Năng lượng hạt nhân có thể gây ô nhiễm môi trường.

→ Phát biểu không đúng là: Năng lượng hạt nhân không thể gây ô nhiễm môi trường

Điện lượng cần nạp cho Pin:

\(q=I.t=2900\,mA.h=2,9\,A.h=10440\text{ }\left( A.s \right)\)

Năng lượng cần nạp cho Pin:

\(\text{W}=q.U=10440.5=52\,200\text{ }J\)

Công suất nạp cho pin:

\(P=U.I=5.1=5\,\left( \text{W} \right)\)

Do có hao phí 25% nên công suất nạp vào chỉ là:

\({{P}_{v}}=0,75.P=0,75.5=3,75\,\left( \text{W} \right)\)

Thời gian nạp: \(t=\dfrac{\text{W}}{{{P}_{v}}}=\dfrac{52\,200}{3,75}=13990s=3h52ph\)

Điện lượng cần nạp cho Pin:

\(q=I.t=2900\,mA.h=2,9\,A.h=10\,440\text{ }\left( A.s \right)\)

Năng lượng cần nạp cho Pin:

\(\text{W}=q.U=10440.5=52\,200\text{ }J\)

Công suất nạp cho pin:

\(P=U.I=5.1=5\,\left( \text{W} \right)\)

Vì không có hao phí trong quá trình nạp nên công suất nạp vào:

\({{P}_{v}}=P=5\,\left( \text{W} \right)\)

Thời gian nạp: \(t=\dfrac{\text{W}}{{{P}_{v}}}=\dfrac{52\,200}{5}=10440s=2h54ph\)

Bộ sạc điện USB Power Adapter A1385 có: Ouput: 5V; 1A

→ Hiệu điện thế đặt vào hai đầu pin của Iphone này là 5V.

Số vân sáng trong miền giao thoa được xác định bởi:

\( - \frac{L}{2} \le ki \le \frac{L}{2}\)

\( \Leftrightarrow  - \frac{{12,5}}{2} \le 1,5k \le \frac{{12,5}}{2}\)

\( \Leftrightarrow  - 4,16 \le k \le 4,16\)

Suy ra có 9 vân sáng.

Số vân tối trong miền giao thoa được xác định bởi:

\( - \frac{L}{2} \le \left( {k + 0,5} \right)i \le \frac{L}{2}\)

\( \Leftrightarrow  - \frac{{12,5}}{2} \le \left( {k + 0,5} \right)1,5 \le \frac{{12,5}}{2}\)

\( \Leftrightarrow  - 4,66 \le k \le 3,66\)

Suy ra có 8 vân tối

Vậy tổng \(N = {N_S} + {N_T} = 9 + 8 = 17\) vân

Vị trí vân tối được xác định theo biểu thức:

\({x_t} = \left( {k + \frac{1}{2}} \right)i \Rightarrow k = \frac{{{x_t}}}{i} - \frac{1}{2} = 3\)

Ứng với k = 3 là vân tối thứ 4

Khoảng cách giữa 5 vân sáng liên tiếp là:

\(x = 4i \Leftrightarrow i = \frac{6}{4} = 1,{5.10^{ - 3}}m\)

Mà

\(\begin{array}{l}i = \frac{{\lambda D}}{a} \Leftrightarrow 1,{5.10^{ - 3}} = \frac{{\lambda .2,5}}{{{{1.10}^{ - 3}}}} = {6.10^{ - 7}}m\\ = 0,6\mu m\end{array}\)

Vận tốc dao động cực đại của phần tử môi trường tại M là:

\({v_{ma{\rm{x}}}} = A\omega  = A.\dfrac{{2\pi }}{T} = 0,5.\dfrac{{2\pi }}{{0,25}} = 4\pi \left( {cm/s} \right)\)

Độ lệch pha dao động của hai phần tử môi trường tại N và P là:

\(\Delta \varphi  = 2\pi \dfrac{{\left| {NM - PM} \right|}}{\lambda } = 2\pi \dfrac{{\left| {5 - 20} \right|}}{{10}} = 3\pi \)

Từ dữ kiện ta có chu kỳ của sóng T = 0,25s

Khoảng cách giữa hai gợn lồi liên tiếp là \(\lambda \)\( \Rightarrow \lambda  = 10cm\)

Ta có: \(\lambda  = v.T \Rightarrow v = \dfrac{\lambda }{T} = \dfrac{{10}}{{0,25}} = 40cm/s\)

Bề mặt chậm nhất là bề mặt gây ra nhiều thời gian nhất để bóng đi xuống đường dốc. Có thể thấy trong mọi quãng đường, thời gian trên bề mặt thảm đi xuống dốc lâu hơn => bề mặt chậm nhất là thảm.

Tỉ số vòng dây ở cuộn sơ cấp và cuộn thứ cấp theo dự định: \(\dfrac{{{N_1}}}{{{N_2}}} = 2 \Rightarrow \dfrac{{{N_2}}}{{{N_1}}} = \dfrac{1}{2}\left( 1 \right)\)

Tỉ số vòng dây ở cuộn sơ cấp và cuộn thứ cấp khi thiếu n vòng: \(\dfrac{{{N_2} - n}}{{{N_1}}} = \dfrac{{{U_2}}}{{{U_1}}} = 0,33\left( 2 \right)\)

Tỉ số vòng dây ở cuộn sơ cấp và cuộn thứ cấp khi thêm 20 vòng: \(\dfrac{{{N_2} - n + 20}}{{{N_1}}} = \dfrac{{U{'_2}}}{{{U_1}}} = 0,38\left( 3 \right)\)

Từ (1) (2) và (3) ta có: \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{{{N_2}}}{{{N_1}}} = \dfrac{1}{2}}\\{\dfrac{{{N_2} - n}}{{{N_1}}} = 0,33}\\{\dfrac{{{N_2} - n + 20}}{{{N_1}}} = 0,38}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\dfrac{n}{{{N_1}}} = \dfrac{{17}}{{100}}}\\{\dfrac{{20}}{{{N_1}}} = \dfrac{1}{{20}}}\end{array}} \right.\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{N_1} = 400}\\{n = 68}\end{array}} \right.\)

Số vòng dây cần quấn thêm là: 68-20=48 vòng

Một phương pháp khả thi để giải quyết vấn đề này là kéo dài đoạn thẳng cho mặt kính lên 50cm. Điều này sẽ xảy ra trong khoảng 6,25 giây. Một phương pháp khác để giải quyết vấn đề này là lưu ý rằng khoảng cách càng dài thì thời gian càng dài. Điều này sẽ loại bỏ 2,75 giây, 3,75 giây và 4,5 giây vì chúng ngắn hơn thời gian 5 giây ở khoảng cách 40cm => câu trả lời đúng là 6,25 giây.

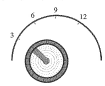
Tỉ số các điện áp hiệu dụng ở cuộn thứ cấp và cuộn sơ cấp là: \(\dfrac{{{N_2}}}{{{N_2}}} = \dfrac{{{U_2}}}{{{U_1}}}\)

\(\begin{array}{l} \Rightarrow {\left( {\dfrac{{{N_1}}}{{{N_2}}}} \right)_{ma{\rm{x}}}} \Leftrightarrow {\left( {{U_2}} \right)_{\min }} = 3v\\ \Rightarrow {\left( {\dfrac{{{N_1}}}{{{N_2}}}} \right)_{ma{\rm{x}}}} = \dfrac{{{U_1}}}{{{U_{2\min }}}} = \dfrac{{220}}{3}\end{array}\)

Vì quãng đường đi được, góc dốc và quả bóng đều như nhau. Điều duy nhất ảnh hưởng đến thời gian là ma sát do bề mặt của đoạn đường nối. Ma sát sẽ làm cho quả bóng chuyển động châm hơn xuống dốc và tăng thời gian đi được quãng đường đã đo. Do đó, ma sát ít nhất sẽ gây ra thời gian đi ngắn nhất. Thời gian vật đi trên kính là ngắn nhất.

Máy biến áp chỉ làm biến đổi điện áp xoay chiều mà không làm thay đổi tần số của nó nên điện áp giữa hai đầu cuộn thứ cấp của máy bằng tần số dòng điện trong cuộn sơ cấp.