Viết phương trình dao động điều hòa
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Một vật nhỏ dao động điều hòa dọc theo trục Ox với biên độ $5cm$, chu kỳ $2s$. Tại thời điểm $t = 0$, vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là
Ta có:
$\begin{gathered}A = 5cm \hfill \\T = 2{\text{s}} \to \omega = \frac{{2\pi }}{T} = \pi ra{\text{d}}/s \hfill \\\end{gathered} $
Tại t=0 $\left\{ \begin{gathered}x = 0 \hfill \\ v > 0 \hfill \\\end{gathered} \right. \leftrightarrow \left\{ \begin{gathered}{\text{cos}}\varphi = 0 \hfill \\\sin \varphi < 0 \hfill \\\end{gathered} \right. \to \varphi = - \frac{\pi }{2}$
$ \to x = Ac{\text{os(}}\omega {\text{t + }}\varphi {\text{) = 5cos(}}\pi {\text{t - }}\frac{\pi }{2})cm$
Một chất điểm dao động điều hoà với phương trình dạng \(x = cos\left( {2\pi t + \frac{\pi }{6}} \right)\left( {cm,{\text{ }}s} \right)\). Lấy ${\pi ^2} = 10$, biểu thức gia tốc tức thời của chất điểm là:
Ta có: $a = - {\omega ^2}Acos(\omega t + \varphi ) = {\omega ^2}Acos(\omega t + \varphi + \pi )$
x = cos(2πt + π/6) (cm, s) $ \to a = - {(2\pi )^2}.1cos(2\pi t + \frac{\pi }{6}) = - 40cos(2\pi t + \frac{\pi }{6})$
Phương trình dao động điều hòa có dạng \(x = Acos\omega t\). Gốc thời gian được chọn là:
Từ phương trình dao động, ta có:
Gốc thời gian $t = 0$:
$x = Ac{\text{os0 = A}}$
Phương trình dao động của một vật có dạng $x = A\sin (\omega t + \frac{\pi }{4})$.Chọn kết luận đúng?
Ta có: $x = A\sin \left( {\omega t + \dfrac{\pi }{4}} \right) = Ac{\text{os}}\left( {\omega t + \dfrac{\pi }{4} - \dfrac{\pi }{2}} \right) = Ac{\text{os}}\left( {\omega t - \dfrac{\pi }{4}} \right)$
- Biên độ dao động của vật là $A$
- Pha ban đầu: \(\varphi = - \dfrac{\pi }{4}\)
Một vật nhỏ dao động theo phương trình $x = Acos(ωt + φ) (cm)$. Tại thời điểm ban đầu, vật đi qua vị trí có li độ $x < 0$, hướng ra xa vị trí cân bằng. Giá trị của $φ$ thỏa mãn:
Tại $t = 0$, ta có $x < 0$ và hướng ra xa vị trí cân bằng $=> v < 0$
$ \leftrightarrow \left\{ \begin{array}{l}
Ac{\rm{os}}\varphi {\rm{ < 0}}\\
v = - A\omega \sin \varphi < 0
\end{array} \right. \to \left\{ \begin{array}{l}
c{\rm{os}}\varphi {\rm{ < 0}}\\
\sin \varphi > 0
\end{array} \right. \to \frac{\pi }{2} < \varphi < \pi $
Một vật dao động điều hòa với biên độ $A = 8 cm$. Tại thời điểm $t = 0$, vật có li độ $x = -4 cm$ và đang đi theo chiều âm của trục $Ox$. Pha ban đầu của dao động bằng:
Ta có: tại t = 0:
\(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi {\rm{ = - 4}}\\v = - A\omega \sin \varphi < 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = - \dfrac{4}{8} = - \dfrac{1}{2}\\\sin \varphi > 0\end{array} \right. \to \varphi = \dfrac{{2\pi }}{3}\)
Cho một chất điểm dao động điều hòa với tần số $1Hz$, thời điểm đầu vật qua vị trí $x = 5cm$ theo chiều dương với tốc độ \(v = 10\pi cm/s\). Viết phương trình dao động.
Ta có:
Tốc độ góc: $\omega = 2\pi f = 2\pi .1 = 2\pi (ra{\rm{d}}/s)$
Biên độ dao động:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {5^2} + {\left( {\frac{{10\pi }}{{2\pi }}} \right)^2} \to A = 5\sqrt 2 cm\)
Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 5\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{5}{{5\sqrt 2 }}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{4}\)
=> \(x = 5\sqrt 2 {\rm{cos}}\left( {2\pi t - \frac{\pi }{4}} \right)cm = 5\sqrt 2 \sin \left( {2\pi t - \frac{\pi }{4} + \frac{\pi }{2}} \right) = 5\sqrt 2 \sin \left( {2\pi t + \frac{\pi }{4}} \right)cm\)
Một vật dao động điều hoà dọc theo trục $Ox$ nằm ngang, gốc $O$ và mốc thế năng ở vị trí cân bằng. Thời gian vật đi từ VTCB đến $A$ hết $0,5s$ và đi hết quãng đường $4cm$ Chọn \(t=0\) lúc vật qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là:
Ta có: Thời gian vật đi từ VTCB đến $A$ là :
\(\frac{T}{4} = 0,5 \to T = 2{\rm{s}} \to \omega = \frac{{2\pi }}{T} = \pi ra{\rm{d}}/s\)
Biên độ A = 4cm
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 0\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = 0\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{2}\)
\( \to x = 4c{\rm{os}}\left( {\pi t - \frac{\pi }{2}} \right)cm\)
Vật nặng dao động điều hòa với \(\omega = 10\sqrt 5 rad/s\). Chọn gốc tọa độ trùng với vị trí cân bằng của vật. Biết rằng tại thời điểm ban đầu vật đi qua li độ $x = 2cm$ với vận tốc \(v = 20\sqrt {15} cm/s\). Phương trình dao động của vật là:
Ta có: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {2^2} + \frac{{{{\left( {20\sqrt {15} } \right)}^2}}}{{{{\left( {10\sqrt 5 } \right)}^2}}} = 16 \to A = 4cm\)
Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 2\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{2}{4} = \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{3}\)
\( \Rightarrow x = 4c{\rm{os}}\left( {10\sqrt 5 t - \frac{\pi }{3}} \right)cm\)
Một vật dao động điều hòa với biên độ $A = 8cm$ và $ω = π rad/s$. Tại thời điểm ban đầu vật qua vị trí có li độ \({x_0} = {\text{ }}4cm\) theo chiều âm. Phương trình dao động của vật là:
Ta có A =8cm, ω = π rad/s
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 4\\{\rm{v = - A}}\omega {\rm{sin}}\varphi < 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{{{x_0}}}{A} = \frac{4}{8} = \frac{1}{2}\\\sin \varphi > 0\end{array} \right. \to \varphi = \frac{\pi }{3}\)
=> x =8cos(πt +π/3)(cm)
Một vật dao động điều hòa trên quỹ đạo dài $8cm$ với chu kì $T=2s$. Chọn gốc thời gian là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là :
Ta có: $L=2A = 8cm => A = 4cm$
Tần số góc: $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{2} = \pi ra{\rm{d}}/s$
Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 0\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = 0\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{2}\)
=> $x{\rm{ }} = {\rm{ }}4cos\left( {\pi t - \frac{\pi }{2}} \right)$
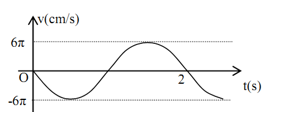
Đồ thị vận tốc của một vật cho ở hình bên, phương trình nào dưới đây là phương trình dao động của vật:
Từ đồ thị, ta có: $T{\rm{ }} = {\rm{ }}2s \to \omega = \frac{{2\pi }}{T} = \pi ra{\rm{d}}/s$
$A\omega = 6\pi cm/s \to A = \frac{{6\pi }}{\omega } = \frac{{6\pi }}{\pi } = 6cm$
Tại t = 0: \({\rm{v = - A}}\omega {\rm{sin}}\varphi = 0 \to \sin \varphi = 0 \to \left[ \begin{array}{l}\varphi = 0\\\varphi = \pi \end{array} \right.\)
và đang đi theo chiều âm\( \to \varphi = 0\)
\( \Rightarrow x = 6c{\rm{os}}\left( {\pi t} \right)cm\)

