Các đại lượng đặc trưng của dao động điều hòa

Ta có:

Độ dài quỹ đạo của vật trong dao động điều hòa: $L=2A$ <=> $MN=2A=30cm$

$=> A=15cm$

Ta có: $x = {\text{ }} - 5cos(5\pi t{\text{ }} - \frac{{7\pi }}{6}) = 5cos(5\pi t{\text{ }} - \frac{{7\pi }}{6} + \pi ) = 5cos(5\pi t{\text{ }} - \frac{\pi }{6})cm$

=> Biên độ: $A=5 cm$, pha ban đầu: $\varphi  =  - \frac{\pi }{6}$

Ta có:

Quãng đường vật đi trong một chu kỳ dao động là $4A$

Quãng đường vật đi được trong nửa chu kỳ dao động là $2A$

Độ dời lớn nhất của vật trong quá trình dao động là $A$

Độ dài quỹ đạo chuyển động của vật là $2A$

Phương trình dao động của vật: \(x = Acos\left( {\pi t} \right)\)

Tại thời điểm ban đầu \(t = 0\), ta có: \(x = Acos\left( {\pi .0} \right) = Acos0 = A\)

=> Lúc \(t = 0\) vật ở vị trí li độ cực đại thuộc phần dương của trục Ox

Ta có: $T = \dfrac{{\Delta t}}{N}$thay số vào ta được: $T = \dfrac{{\Delta t}}{N} = \dfrac{{20}}{{80}} = 0,25{\text{s}}$

Ta có:

$\begin{gathered}x = 4c{\text{os(10}}\pi {\text{t + }}\frac{\pi }{3}) \hfill \\v =  - 40\pi \sin (10\pi t + \frac{\pi }{3}) \hfill \\\end{gathered} $

Tại $t=0,5s$ thay vào phương trình trên $ \to x =  - 2cm,{\text{ v = 20}}\pi \sqrt 3 {\text{ cm/s}}$ 

Ta có: $\omega  = \frac{{2\pi }}{T} = 2\pi f \to \left\{ \begin{gathered}T = \frac{{2\pi }}{\omega } \hfill \\f = \frac{\omega }{{2\pi }} \hfill \\\end{gathered}  \right.$

Từ phương trình, ta có: $ω=20π$, thay vào công thức trên => $\left\{ \begin{gathered}T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{20\pi }} = 0,1{\text{s}} \hfill \\f = \frac{\omega }{{2\pi }} = \frac{1}{T} = 10H{\text{z}} \hfill \\\end{gathered}  \right.$

Ta có:

+ Chu kì dao động của vật: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1{\rm{s}}\)

\(\Delta t = 2s = 2T\)

+ Trong 1 chu kì vật đi được quãng đường \(4A\)

=> Quãng đường vật đi được sau \(2s\) là:  \(2.4A = 40{\rm{ }}cm\)

Tại li độ $x=3cm$, ta có:

${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \leftrightarrow {5^2} = {3^2} + \dfrac{{{v^2}}}{{{{\left( {2\pi } \right)}^2}}} \to v = 8\pi  = 25,12cm/s$

Li độ của chất điểm khi pha dao động bằng \(\dfrac{{2\pi }}{3}\)  là: \(x = 6cos(\dfrac{{2\pi }}{3}) =  - 3{\rm{ }}cm\)

Ta có: x.v < 0, có thể xảy ra 2 TH

+ x > 0,v < 0 : Vật đi từ A => 0: Vật đang chuyển động danh dần theo chiều âm

+ x < 0, v > 0: Vật đi từ -A=> 0: Vật đang chuyển động nhanh dần theo chiều dương

=> x.v <0: Vật đang chuyển động nhanh dần về vị trí cân bằng

Ta có: $\left\{ \begin{gathered}{v_{{\text{max}}}} = \omega A \hfill \\{a_{{\text{max}}}} ={\omega ^2}A \hfill \\\end{gathered}  \right. \to \left[ {\dfrac{{{a_{{\text{max}}}}}}{{{v_{{\text{max}}}}}} = \dfrac{{{\omega ^2}A}}{{\omega A}} = \omega  = \dfrac{{16{\pi ^2}}}{{8\pi }} = 2\pi  = 2\pi f \to f = \dfrac{\omega }{{2\pi }}} \right. = 1H{\text{z}}$

Ta có: $\left\{ \begin{gathered}{v_{{\text{max}}}} = \omega A \hfill \\{a_{{\text{max}}}} = {\omega ^2}A \hfill \\\end{gathered}  \right. \to \dfrac{{{v^2}_{{\text{max}}}}}{{{a_{{\text{max}}}}}} = \dfrac{{{{(\omega A)}^2}}}{{{\omega ^2}A}} = A = \dfrac{{{{\left( {16\pi } \right)}^2}}}{{64\pi^2 }} = 4cm$

Ta có: $a =  - {\omega ^2}Acos(\omega t + \varphi ) = {\omega ^2}Acos(\omega t + \varphi  + \pi )$

x = cos(2πt + π/6) (cm, s) $ \to a =  - {(2\pi )^2}.1cos(2\pi t + \dfrac{\pi }{6}) =  - 40cos(2\pi t + \dfrac{\pi }{6})$

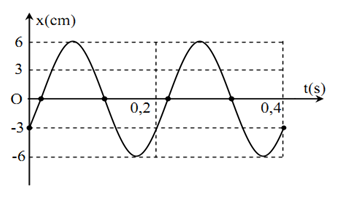
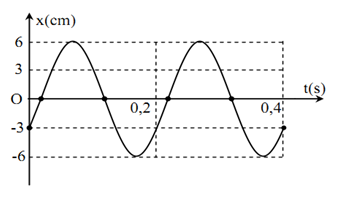
Ta có:

$\begin{gathered}A = 6cm \hfill \\2T = 0,4{\text{s}} \to T = 0,2{\text{s}} \to \omega {\text{ = }}\frac{{2\pi }}{T} = 10\pi ra{\text{d}}/s \hfill \\\end{gathered} $

$ \to {v_{{\text{max}}}} = A\omega  = 60\pi cm/s$

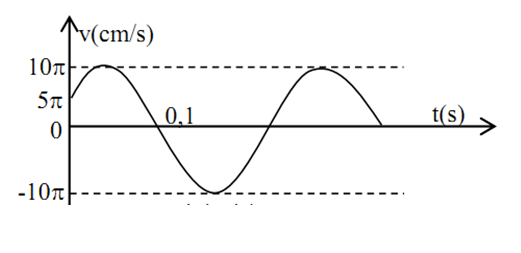
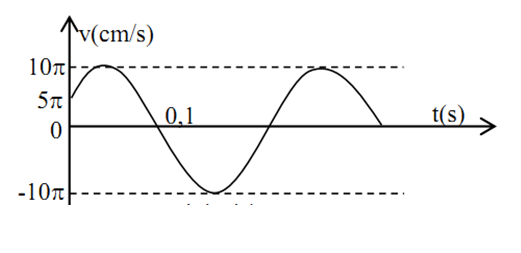
Ta có:

$\left\{ \begin{gathered}A\omega  = 10\pi cm/s \hfill \\\dfrac{{5T}}{{12}} = 0,1{\text{s}} \to T = 0,24{\text{s}} \to \omega  = \dfrac{{25\pi }}{3}ra{\text{d}}/s \hfill \\\end{gathered}  \right.$

Tại \(t = 0\): \(\left\{ \begin{array}{l}v = 5\pi \\v > 0\end{array} \right. \leftrightarrow \left\{ \begin{array}{l} - A\omega \sin \varphi {\rm{ = 5}}\pi \\{\rm{sin}}\varphi  < 0\end{array} \right. \leftrightarrow \left\{ \begin{array}{l}\sin \varphi {\rm{ = }}\dfrac{{{\rm{ - 5}}\pi }}{{10\pi }} = \dfrac{{{\rm{ - 1}}}}{2}\\{\rm{sin}}\varphi  < 0\end{array} \right. \to \varphi  = \left[ \begin{array}{l} - \dfrac{\pi }{6}\\\dfrac{{7\pi }}{6}\end{array} \right.\)

Mặt khác, vận tốc đang tăng => \(\varphi  = \dfrac{{7\pi }}{6}\)

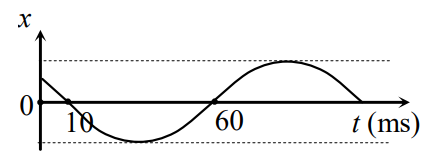
Từ đồ thị ta thấy trong khoảng thời gian từ 10 ms đến 60 ms, vật thực hiện được \(\frac{1}{2}\) chu kì:

\(\frac{T}{2} = 60 - 10 \Rightarrow T = 100\,\,\left( {ms} \right) = 0,1\,\,\left( s \right)\)