Sóng âm

Sóng âm trong môi trường lỏng, khí là sóng dọc; trong môi trường rắn là sóng dọc hoặc sóng ngang.

Âm nghe được (âm thanh) là sóng cơ học có tần số nằm trong khoảng $16 Hz- 20000 Hz$

Ta có:

$f = \dfrac{1}{T} = \dfrac{1}{{0,08}} = 12,5H{\text{z < 16Hz}}$

=> Hạ âm

Ta có:Âm nghe được có tần số từ 16 Hz - 20000 Hz

Tần số âm $f = \dfrac{1}{T}$

A: f = 500kHz

B: f = 500Hz

C: f = 30kHz

D: f =10Hz

Vận tốc truyền âm phụ thuộc vào tính đàn hồi, mật độ của môi trường và nhiệt độ của môi trường.

v_R > v_L > v_K

Hai âm có âm sắc khác nhau khi chúng có các họa âm có tần số và biên độ khác nhau

Ta có, chiều dài của dây đàn:

$l = k\dfrac{\lambda }{2} = k\dfrac{v}{{2f}} \to f = k\dfrac{v}{{2l}}$

Âm cơ bản là âm ứng với $k=1$

=> Tần số của âm cơ bản:

${f_1} = \dfrac{v}{{2l}} = \dfrac{{300}}{{2.0,15}} = 1000H{\text{z}}$

=> Bước sóng của âm phát ra trong không khí:

$\lambda  = \dfrac{{{v_{kk}}}}{{{f_1}}} = \dfrac{{340}}{{1000}} = 0,34m$

Các đặc trưng vật lí của sóng âm: tần số, vận tốc, bước sóng, năng lượng âm, cường độ âm và mức cường độ âm.

Các đặc trưng sinh lý của âm gồm: độ cao, độ to và âm sắc

Ta có, mức cường độ âm: $L = \log \dfrac{I}{{{I_0}}} = \log \dfrac{{{{10}^{ - 5}}}}{{{{10}^{ - 12}}}} = 7B = 70dB$

Gọi công suất mỗi nguồi là P

Cường độ âm tại B do A gây ra:

${I_{AB}} = \dfrac{{4P}}{{4\pi {d^2}}} = {10^{ - 6}}W/{m^2}$

Cường độ âm tại B do C gây ra:

${I_{CB}} = \dfrac{{6P}}{{4\pi {{(\dfrac{{2d}}{3})}^2}}} = \dfrac{{4P}}{{4\pi {d^2}}}\dfrac{{27}}{8} = 3,{375.10^{ - 6}}W/{m^2}$

$\to {L_B} = \log \dfrac{{{I_{CB}}}}{{{{10}^{ - 12}}}} = 6,528B = 65,28dB$

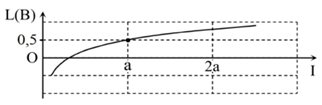
Từ đồ thị ta thấy khi $I=a$ thì $L=0,5\,\left( B \right)$

Áp dụng công thức tính mức cường độ âm ta có:

$L\,\left( B \right)=\log \frac{I}{{{I}_{0}}}\Rightarrow \frac{I}{{{I}_{0}}}={{10}^{L}}\Rightarrow {{I}_{0}}=\frac{I}{{{10}^{L}}}=\frac{a}{{{10}^{0,5}}}=0,316a$

Ta có:

$\begin{array}{l}\left\{ \begin{array}{l}L = 10.\log \dfrac{I}{{{I_0}}}\,\,\left( {dB} \right)\\L' = 10.\log \dfrac{{I'}}{{{I_0}}}\,\,\left( {dB} \right) = 10.\log \dfrac{{1000.I}}{{{I_0}}} = 10.\log 1000 + 10.\log \dfrac{I}{{{I_0}}}\,\end{array} \right.\\ \Rightarrow L' = L + 30\,\left( {dB} \right)\end{array}$

Từ phương trình sóng ta có: $\Delta \varphi =\dfrac{2\pi x}{\lambda }=kx\Rightarrow \lambda =\dfrac{2\pi }{k}$

Lại có: $\omega =f\Rightarrow T=\dfrac{2\pi }{\omega }=\dfrac{2\pi }{f}$

Vận tốc sóng âm là: $v=\dfrac{\lambda }{T}=\dfrac{\dfrac{2\pi }{k}}{\dfrac{2\pi }{f}}=\dfrac{f}{k}.$

Ta có hiệu hai mức cường độ âm:

$\begin{align}& {{L}_{A}}-{{L}_{B}}=10\log \frac{{{I}_{A}}}{{{I}_{B}}}=10\log {{\left( \frac{OB}{OA} \right)}^{2}} \\& \Rightarrow 55-35=10\log {{\left( \frac{OB}{OA} \right)}^{2}}=20 \\& \Rightarrow \log {{\left( \frac{OB}{OA} \right)}^{2}}=2\Rightarrow {{\left( \frac{OB}{OA} \right)}^{2}}={{10}^{2}} \\& \Rightarrow OB=10OA=50\,\,\left( m \right) \\\end{align}$