Chất Iốt phóng xạ \({}_{53}^{131}\)I dùng trong y tế có chu kỳ bán rã 8 ngày đêm. Nếu nhận được 100g chất này thì sau 8 tuần lễ còn bao nhiêu?
t = 8 tuần = 56 ngày = 7.T .Suy ra sau thời gian t thì khối lượng chất phóng xạ \({}_{53}^{131}\)I còn lại là :
\(m = {m_0}{.2^{ - \frac{t}{T}}} = {100.2^{ - 7}}\)= 0,78 gam .
\({}^{22}Na\) phân rã với chu kì T = 2,6 năm. Khối lượng ban đầu là m0. Sau 2 năm lượng \({}^{22}Na\) phân rã bao nhiêu %?
t = 2 năm, T = 2,6 năm
Ta có: khối lượng hạt nhân đã phân rã: \(\Delta m{\rm{ }} = {m_0}(1 - {2^{ - \frac{t}{T}}}) \to \frac{{\Delta m}}{{{m_0}}} = 1 - {2^{ - \frac{t}{T}}} = 1 - {2^{ - \frac{2}{{2,6}}}} = 0,4133 = 41,33\% \)
Tính số hạt nhân bị phân rã sau 1s trong 1g Rađi \({}^{226}\)Ra . Cho biết chu kỳ bán rã của \({}^{226}\)Ra là 1580 năm. Số Avôgađrô là NA = 6,02.1023 mol-1.
Số hạt nhân nguyên tử có trong 1 gam 226Ra là :
\(N_0=\dfrac{m}{A}.{N_A} = \dfrac{1}{{226}}.6,{022.10^{23}} = 2,{6646.10^{21}}\) hạt
Suy ra số hạt nhân nguyên tử Ra phân rã sau 1 s là :
\(\Delta N = {N_0}(1 - {2^{ - \dfrac{t}{T}}}) = 2,{6646.10^{21}}\left( {1 - {2^{ - \dfrac{1}{{1580.365.86400}}}}} \right) = 3,{70.10^{10}}\) hạt
Pôlôni \(^{210}Po\) là một chất phóng xạ có chu kì bán rã \(140\) ngày đêm. Hạt nhân pôlôni phóng xạ sẽ biến thành hạt nhân chì (\(^{206}Pb\)) và kèm theo một hạt a. Ban đầu có \(42 mg\) chất phóng xạ pôlôni. Khối lượng chì sinh ra sau \(280\) ngày đêm là:
Ta có:
\({m_{Pb}} = \dfrac{{\Delta {m_{Po}}}}{{{A_{Po}}}}.{A_{Pb}} \\= {m_0}\dfrac{{{A_{Pb}}}}{{{A_{Po}}}}(1 - {2^{\dfrac{t}{T}}}) \\= 42\dfrac{{206}}{{210}}(1 - {2^{ - \dfrac{{280}}{{140}}}}) = 30,9mg\)
Đồng vị \({}_{11}^{24}\) Na là chất phóng xạ β- tạo thành hạt nhân magiê( \({}_{12}^{24}\)Mg). Ban đầu có 12gam Na và chu kì bán rã là 15 giờ. Sau 45 h thì khối lượng Mg tạo thành là :
Nhận xét : t = 3T nên ta dùng hàm mũ 2 để giải cho nhanh bài toán :
- Khối lượng Na bị phân rã sau t = 45 giờ = 3T :
\(\begin{array}{l}\Delta m = {m_0}(1 - {2^{ - \dfrac{t}{T}}}) = 12(1 - {2^{ - 3}})\\ \leftrightarrow \Delta m{\rm{ }} = {\rm{ }}10,5{\rm{ }}g\end{array}\)
- Suy ra khối lượng của Mg tạo thành : \({m_{con}} = \dfrac{{\Delta {m_{me}}.{A_{con}}}}{{{A_{me}}}} = \frac{{10,5}}{{24}}.24 = 10,5g\)
Một lượng chất phóng xạ sau 12 năm thì còn lại 1/16 khối lượng ban đầu của nó. Chu kì bán rã của chất đó là
Ta có \(\frac{m}{{{m_0}}}\)=\(\frac{1}{{{2^{\frac{t}{T}}}}}\)=\(\frac{1}{{16}} = \frac{1}{{{2^4}}}\)
\( \to \frac{t}{T} = 4 \Rightarrow T = \frac{t}{4} = \frac{{12}}{4} = 3\) năm
Một đồng vị phóng xạ có chu kì bán rã T. Cứ sau một khoảng thời gian bằng bao nhiêu thì số hạt nhân bị phân rã trong khoảng thời gian đó bằng ba lần số hạt nhân còn lại của đồng vị ấy
Theo đề , ta có :\(\Delta N = 3N\)
\(\dfrac{{\Delta N}}{N} = \dfrac{{{N_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)}}{{{N_0}{{.2}^{ - \dfrac{t}{T}}}}} = 3 \Leftrightarrow {2^{\dfrac{t}{T}}} - 1 = 3 \Leftrightarrow {2^{\dfrac{t}{T}}} = 4 \Leftrightarrow t = 2T\)
\(_{11}^{24}Na\) là chất phóng xạ \({\beta ^ - }\) với chu kỳ bán rã 15 giờ. Ban đầu có một lượng \(_{11}^{24}Na\) thì sau một khoảng thời gian bao nhiêu lượng chất phóng xạ trên bị phân rã 75%?
Gọi m0 là khối lượng ban đầu của \(_{11}^{24}Na\)
Khối lượng chất phóng xạ đã bị phân rã:
\(\Delta m = {m_0}(1 - {2^{ - \frac{t}{T}}})\)
Theo đầu bài, ta có: ∆m=0,75m0
\( \to \dfrac{{\Delta m}}{{{m_0}}} = (1 - {2^{ - \dfrac{t}{T}}}) = 0,75 \to {2^{ - \dfrac{t}{T}}} = \dfrac{1}{4} \to \dfrac{t}{T} = 2 \to t = 2T = 30h00\)
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã \(T\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \({\rm{\Delta N}}\) và số hạt ban đầu \({{\rm{N}}_{\rm{0}}}{\rm{.}}\) Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?
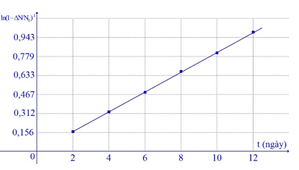
Ta có: \(N = {N_0}{e^{ - \lambda t}} \Rightarrow \)Số hạt bị phân rã là:
\(\Delta N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}(1 - {e^{ - \lambda t}})\)
\( \Rightarrow \dfrac{{\Delta N}}{{{N_0}}} = 1 - {e^{ - \lambda t}} \Rightarrow 1 - \dfrac{{\Delta N}}{{{N_0}}} = {e^{ - \lambda t}}\)
\( \Rightarrow \dfrac{1}{{\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)}} = {e^{\lambda t}} \Rightarrow \ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\)
Từ đồ thị ta thấy \(\lambda \approx 0,078\)
\( \Rightarrow T = \dfrac{{\ln 2}}{\lambda } \approx 8,9\) (ngày)
Coban \({}_{27}^{60}Co\) là chất phóng xạ có chu kì bán rã T = 5,33 năm. Lúc đầu có 1000g Co thì sau 10,66 năm số nguyên tử coban còn tại là?
Khối lượng Co còn lại sau 10,66 năm là:
\(m = {m_0}{.2^{ - \dfrac{t}{T}}} = {1000.2^{ - \dfrac{{10,66}}{{5,33}}}} = 250g\)
Số nguyên tử Coban còn lại là:
\(N = \dfrac{m}{A}.{N_A} = \dfrac{{250}}{{60}}.6,{02.10^{23}} = 2,{51.10^{24}}\)
Chất phóng xạ pôlôni \({}_{84}^{210}Po\) có chu kì bán rã 138 ngày. Ban đầu có một mẫu gồm N0 hạt nhân pôlôni \({}_{84}^{210}Po\). Sau bao lâu (kể từ lúc ban đầu), số hạt nhân \({}_{84}^{210}Po\) bị phân rã là \(\dfrac{7}{8}{N_0}\)?
Số hạt nhân bị phân rã là: \(\Delta N = \dfrac{7}{8}{N_0}\)
Số hạt nhân còn lại là: \(N\left( t \right) = {N_0} - \Delta N = {N_0} - \dfrac{7}{8}{N_0} = \dfrac{1}{8}{N_0}\)
\( \Rightarrow {N_0}{.2^{ - \dfrac{t}{T}}} = \dfrac{1}{8}{N_0} \Rightarrow {2^{ - \dfrac{t}{T}}} = \dfrac{1}{8} = {2^{ - 3}} \Rightarrow \dfrac{t}{T} = 3 \Rightarrow t = 3T = 3.138 = 414\) (ngày)

