Con lắc lò xo

A, C, D đúng

B - sai vì gia tốc của vật luôn luôn thay đổi mà chuyển động biến đổi đều là chuyển động có gia tốc không đổi

Ta có, cơ năng của con lắc lò xo dao động điều hòa: \(W = \dfrac{1}{2}k{A^2}\)

=> Cơ năng thỉ lệ thuận với độ cứng k và bình phương biên độ dao động

A, B - đúng vì dao động của con lắc lò xo là dao động điều hòa mà dao động điều hòa là trường hợp riêng của dao động tuần hoàn

D - đúng vì: số dao động vật thực hiện trong 1s là tần số 

\(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \) (tỉ lệ thuận với căn bậc 2 của k)

C - sai vì chu kì dao động không phụ thuộc vào biên độ

Ta có, chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}} \)

=> chu kì T phụ thuộc vào khối lượng m, độ cứng k

Biên độ dao động phụ thuộc vào kích thích ban đầu

Từ phương trình dao động điều hòa, ta có biên độ $A = 4cm$, tần số góc $\omega = 2$

Cơ năng trong dao động điều hòa của chất điểm:

\(W = \dfrac{1}{2}m{\omega ^2}{A^2} = \dfrac{1}{2}0,{1.2^2}.0,{04^2} = 3,{2.10^{ - 4}}J\)

Ta có, tần số dao động của con lắc lò xo: \(f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} \)

Khi tăng khối lượng lên 4 lần và độ cứng tăng 2 lần tức là \(\left\{ \begin{array}{l}m' = 4m\\k' = 2k\end{array} \right.\)

Tần số dao động của con lắc khi này: \(f' = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{k'}}{{m'}}}  = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{2k}}{{4m}}}  = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{{2m}}} \)

\(\dfrac{{f'}}{f} = \dfrac{{\dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{{2m}}} }}{{\dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} }} = \dfrac{1}{{\sqrt 2 }}\)

\( \Rightarrow f' = \dfrac{f}{{\sqrt 2 }}\)

Hay nói cách khác khi tăng khối lượng lên $4$ lần và độ cứng tăng $2$ lần thì tần số dao động sẽ giảm \(\sqrt 2 \) lần

Cơ năng dao động của con lắc lò xo:

\(W = \dfrac{1}{2}k{A^2} \to A = \sqrt {\dfrac{{2{\rm{W}}}}{k}}  = \sqrt {\dfrac{{2.0,12}}{{150}}}  = 0,04m = 4cm\)

Ta có, chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}}  \to {T^2} = 4{\pi ^2}\dfrac{m}{k}\)

=> Đồ thị $T -  m$ có dạng parabol 

Ta có, tần số dao động của con lắc lò xo:

\(f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}}  \to m = \dfrac{k}{{4{\pi ^2}{f^2}}} = \dfrac{{100}}{{4{\pi ^2}{{\left( {3,18} \right)}^2}}} = 0,25kg = 250g\)

Ta có độ dãn của lò xo tại vị trí cân bằng:

\(\Delta l = l - {l_0} = 27,5 - 25 = 2,5cm = 0,025m\)

Chu kì dao động của con lắc lò xo treo thẳng đứng:

\(T = 2\pi \sqrt {\frac{{\Delta l}}{g}}  = 2\pi \sqrt {\frac{{0,025}}{{10}}}  = 0,314s\)

Ta có, độ dãn của lò xo tại vị trí cân bằng:

\(\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,16.10}}{{25}} = 0,064m = 6,4cm\)

Tần số góc dao động của con lắc:

\(\omega  = \sqrt {\dfrac{k}{m}}  = \sqrt {\dfrac{{25}}{{0,16}}}  = 12,5(ra{\rm{d}}/s)\)  

Chu kì dao động của vật:

\(T = 2\pi \sqrt {\dfrac{m}{k}} \)

\( \to \dfrac{{{T_1}}}{{{T_2}}} = \sqrt {\dfrac{{{m_1}}}{{{m_2}}}}  \to {m_2} = \dfrac{{{m_1}T_2^2}}{{T_1^2}} = \dfrac{{4.0,{5^2}}}{{{1^2}}} = 1kg\)

Ta có:

\({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x =  \pm \frac{A}{{\sqrt 2 }}\)

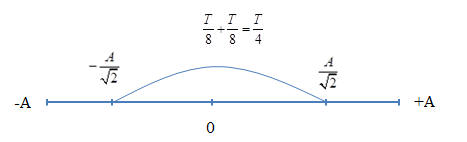
Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\dfrac{T}{4}\)

Theo đầu bài, ta có:

\(\begin{array}{l}\dfrac{\pi }{{40}} = \dfrac{T}{4} \to T = \dfrac{\pi }{{10}}\\\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{\dfrac{\pi }{{10}}}} = 20(ra{\rm{d}}/s)\end{array}\)

Ta có: tần số góc

\(\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{\dfrac{\pi }{5}}} = 10(ra{\rm{d}}/s)\)

Cơ năng của dao động:

\({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2} \to A = \sqrt {\dfrac{{2{\rm{W}}}}{{m{\omega ^2}}}}  = \sqrt {\dfrac{{2.0,02}}{{1{{(10)}^2}}}}  = 0,02m = 2cm\)

Cơ năng ban đầu của con lắc là: \({\rm{W}} = \dfrac{1}{2}k{A^2}\)

Giữ chặt một phần của lò xo, biên độ mới của con lắc và độ cứng của lò xo:

\(k'A' = kA \Rightarrow k' = \dfrac{{kA}}{{A'}}\)

Cơ năng của con lắc giảm 10%, cơ năng còn lại là:

\(\begin{array}{l}{\rm{W}}' = \dfrac{1}{2}k'A{'^2} = 0,9W = 0,9.\dfrac{1}{2}k{A^2}\\ \Rightarrow \dfrac{{kA}}{{A'}}.A{'^2} = 0,9.k{A^2} \Rightarrow A' = 0,9A = A.90\% \\ \Rightarrow A - A' = A.10\% \end{array}\)

Áp dụng định lí bảo toàn cơ năng cho con lắc, ta có:

\(\begin{align}& \text{W}={{\text{W}}_{t}}+{{\text{W}}_{d}}\Rightarrow \frac{1}{2}k{{A}^{2}}=\frac{1}{2}k{{x}^{2}}+{{\text{W}}_{d}} \\& \Rightarrow {{\text{W}}_{d}}=\frac{1}{2}k{{A}^{2}}-\frac{1}{2}k{{x}^{2}}=0,009\,\,\left( J \right) \\\end{align}\)

Ta có:

\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\)

\( \Leftrightarrow \dfrac{1}{2}k{A^2} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{{\rm{x}}^2}\)

Tại VTCB thế năng bằng 0.

Vị trí con lắc có động năng bằng cơ năng => là vị trí động năng cực đại => VTCB.

Tại VTCB, li độ x = 0.