Sóng cơ - Các đại lượng đặc trưng của sóng cơ
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Sóng ngang là:
Sóng ngang: là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
Một người ngồi ở bờ biển quan sát thấy khoảng cách giữa năm ngọn sóng liên tiếp bằng $20 m$. Bước sóng là:
Ta có, khoảng cách giữa năm ngọn sóng liên tiếp là: $4λ = 20 m => λ = 5m$
Sóng ngang:
Sóng ngang truyền trong: Chất rắn và bề mặt chất lỏng.
Một người ngồi ở bờ biển đếm được $20$ ngọn sóng đi qua trước mặt trong $76s$. Chu kì dao động của nước biển là:
Ta có, $20$ ngọn sóng đi qua trước mặt tương đương với $19$ bước sóng hay $19$ chu kì dao động
=> $19T = 76s => T = 4s$
Sóng dọc là:
Sóng dọc: là sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
Sóng dọc:
Sóng dọc truyền trong: tất cả các môi trường rắn, lỏng, khí.
Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số $120 Hz$, tạo ra sóng ổn định trên mặt chất lỏng. Xét $5$ gợn lồi liên tiếp trên một phương truyền sóng ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm $0,5m$. Tính tốc độ truyền sóng trên mặt chất lỏng:
Ta có:
Khoảng cách giữa $5$ gợn lồi (ngọn sóng) là: $4λ = 0,5m => λ = 0,125 m$
\(\lambda = \dfrac{v}{f} \to v = \lambda f = 0,125.120 = 15m/s\)
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm $t$, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục $Ox$. Bước sóng của sóng này bằng:
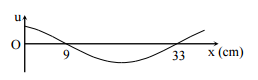
Từ đồ thị, ta có:
\(\dfrac{\lambda }{2} = 33 - 9 = 24cm \to \lambda = 48cm\)
Tốc độ truyền sóng trong một môi trường:
Tốc độ truyền sóng v : là tốc độ lan truyền dao động trong môi trường
Phụ thuộc vào bản chất của môi trường truyền (tính đàn hồi và mật độ môi trường): vR> vL> vK
Một nguồn phát sóng dao động theo phương trình \(u = ac{\rm{os20}}\pi {\rm{t}}\) (cm). Trong khoảng thời gian 2s sóng truyền đi được quãng đường bằng bao nhiêu lần bước sóng?
Ta có:
\(T = \dfrac{{2\pi }}{{20\pi }} = 0,1s\)
2s = 20T
=> Quãng đường sóng truyền đi trong 2s bằng 20 lần bước sóng
Một nguồn dao động điều hoà với chu kỳ 0,04s. Vận tốc truyền sóng bằng 200cm/s. Hai điểm nằm trên cùng một phương truyền sóng và cách nhau 6 cm, thì có độ lệch pha:
Ta có:
Bước sóng:
\(\lambda = vT = 200.0,04 = 8cm\)
Độ lệch pha của hai dao động tại hai điểm là:
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi 6}}{8} = \dfrac{3}{2}\pi \)
Một sóng cơ học lan truyền trong một môi trường A có vận tốc vA và khi truyền trong môi trường B có vận tốc vB = 2vA. Bước sóng trong môi trường B sẽ:
Vì f không thay đổi trong các môi trường
Ta có:
$\lambda = vT = \dfrac{v}{f} \to \dfrac{{{\lambda _A}}}{{{\lambda _B}}} = \dfrac{{{v_A}}}{{{v_B}}} = \dfrac{1}{2} \to {\lambda _B} = 2{\lambda _A}$
Một sóng có tần số $500 Hz$ và tốc độ lan truyền $350 m/s$. Hỏi hai điểm gần nhất trên phương truyền sóng cách nhau một khoảng bao nhiêu để giữa chúng có độ lệch pha \(\dfrac{\pi }{4}\)?
Bước sóng:
\(\lambda = \dfrac{v}{f} = \dfrac{{350}}{{500}} = 0,7m\)
Để độ lệch pha giữa 2 điểm gần nhất là \(\dfrac{\pi }{4}\)
\( \leftrightarrow \Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{\pi }{4} \to d = \dfrac{\lambda }{8} = \dfrac{{0,7}}{8} = 0,0875m = 8,75cm\)
Một nguồn phát sóng cơ dao động với phương trình \(u = 4\cos \left( {4\pi t - \dfrac{\pi }{4}} \right)\left( {{\rm{cm}}} \right)\). Biết dao động tại hai điểm gần nhau nhất trên cùng một phương truyền sóng cách nhau 0,5m có độ lệch pha là \(\dfrac{\pi }{3}\). Tốc độ truyền của sóng đó là
Độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi df}}{v} = \dfrac{\pi }{3}\)
\( \Rightarrow v = 6df = 6d\dfrac{\omega }{{2\pi }} = 6.0,5.\dfrac{{4\pi }}{{2\pi }} = 6\,\,\left( {m/s} \right)\)
Một nguồn phát sóng nước có dạng \(u = A\cos \left( {\dfrac{\pi }{4}t} \right)\,\,\left( {cm} \right)\). Cho tốc độ truyền sóng không đổi. Tại một điểm cách nguồn một khoảng d, độ lệch pha của dao động sóng tại điểm đó ở hai thời điểm cách nhau \(\Delta t = 0,2\,s\) là
Độ lệch pha giữa hai thời điểm là: \(\Delta \varphi = \omega \Delta t = \dfrac{\pi }{4}.0,2 = 0,05\pi \,\,\left( {rad} \right)\)

