Một quả cầu khối lượng \(m = 4g\) treo bằng một sợi chỉ mảnh. Điện tích của quả cầu là \({q_1} = {2.10^{ - 8}}C\). Phía dưới quả cầu dọc theo phương của sợi chỉ có một điện tích \({q_2}\). Khoảng cách giữa hai điện tích là \(r = 5cm\) và lực căng dây là \(T = {5.10^{ - 2}}N\). Xác định điện tích \({q_2}\) và lực tác dụng giữa chúng, lấy \(g = 10m/{s^2}\)
Ta có:
+ Trọng lượng \(P = mg = \dfrac{4}{{1000}}.10 = 0,04N\)
Lực căng dây \(T = {5.10^{ - 2}}N\)
Nhận thấy \(T > P \Rightarrow \) lực tương tác giữa hai điện tích phải có chiều như hình vẽ sau:
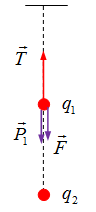
Ta suy ra hai điện tích hút nhau (trái dấu)
Lại có \({q_1} > 0 \Rightarrow {q_2} < 0\)
\(\overrightarrow T + \overrightarrow P + \overrightarrow F = \overrightarrow 0 \)
Chiếu theo phương hướng xuống của sợi dây ta có:
\(\begin{array}{l} - T + P + F = 0\\ \Rightarrow F = T - P = {5.10^{ - 2}} - 0,04 = 0,01N\end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = 0,01N\\ \Rightarrow \left| {{q_2}} \right| = \dfrac{{0,01.0,{{05}^2}}}{{{{9.10}^9}{{.2.10}^{ - 8}}}} = 1,{399.10^{ - 7}}C\end{array}\)
\( \Rightarrow {q_2} = - 1,{39.10^{ - 7}}C\) (do điều kiện \({q_2} < 0\) suy ra ở trên)
Hai quả cầu nhỏ giống hệt nhau bằng kim loại A và B đặt trong không khí, có điện tích lần lượt là q1 = -3,2.10-7 C, q2 = 2,4.10-7 C, cách nhau một khoảng 12 cm. Xác định số electron thừa và thiếu ở mỗi quả cầu?
Số electron thừa ở quả cầu A là: \({n_A} = \left| {\frac{{{q_A}}}{e}} \right| = {2.10^{12}}\,\,\left( {electron} \right)\)
Số electron thiếu ở quả cầu B là: \({n_B} = \left| {\frac{{{q_B}}}{e}} \right| = 1,{5.10^{12}}\,\,\left( {electron} \right)\)
Cho hai quả cầu kim loại nhỏ, giống nhau, tích điện và cách nhau 20 cm thì chúng hút nhau một lực bằng 1,2 N. Cho chúng tiếp xúc với nhau rồi tách chúng ra đến khoảng cách như cũ thì chúng đẩy nhau một lực bằng lực hút. Tính điện tích lúc đầu của mỗi quả cầu
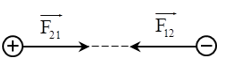
- Hai quả cầu ban đầu hút nhau nên chúng mang điện trái dấu.
- Từ giả thiết bài toán, ta có: \(\left\{ \begin{array}{l}\left| {{q_1}{q_2}} \right| = - {q_1}{q_2} = \frac{{F{r^2}}}{k} = \frac{{16}}{3}{.10^{ - 12}}\\{\left( {\frac{{{q_1} + {q_2}}}{2}} \right)^2} = \frac{{F{r^2}}}{k} \Rightarrow {q_1} + {q_2} = \pm \frac{{\sqrt {192} }}{3}{.10^{ - 6}}\end{array} \right.\)
Theo hệ thức Vi – et thì q1 và q2 là nghiệm của phương trình:
\({q^2} \pm \frac{{\sqrt {192} }}{3}{.10^{ - 6}}q - \frac{{16}}{3}{.10^{ - 12}} = 0 \Rightarrow \left( \begin{array}{l}\left\{ \begin{array}{l}{q_1} = 0,{96.10^{ - 6}}C\\{q_2} = - 5,{58.10^{ - 6}}C\end{array} \right.\\\left\{ \begin{array}{l}{q_1} = - 5,{58.10^{ - 6}}C\\{q_2} = 0,{96.10^{ - 6}}C\end{array} \right.\end{array} \right.\)
Cho hai loại điện tích q1và q2 đặt cách nhau 15cm trong không khí, lực tác dụng giữa chúng là F. Khi đặt chúng trong dầu thì lực này còn bằng F/2,25. Để lực tác dụng vẫn là F thì cần phải dịch chuyển chúng lại một đoạn là
Cách giải :
Ta có :
\(\left\{ \begin{array}{l}F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{0,{{15}^2}}}\\{F_d} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{\varepsilon _d}.0,{{15}^2}}} = \frac{F}{{2,25}}\end{array} \right. \Rightarrow {\varepsilon _d} = 2,25\)
Để lực tác dụng vẫn là F :
\(\left\{ \begin{array}{l}F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{0,{{15}^2}}}\\{F_d} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{\varepsilon _d}.r{'^2}}} = F\end{array} \right. \Rightarrow \frac{{k\left| {{q_1}{q_2}} \right|}}{{2,25.r{'^2}}} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{0,{{15}^2}}} \Leftrightarrow \frac{1}{{2,25.r{'^2}}} = \frac{1}{{0,{{15}^2}}} \Rightarrow r' = 10cm = r - 5cm\)
Cho 4 điện tích \({q_{1\;}} = {q_{3\;}} = {4.10^{ - 6}}C;{q_{2\;}} = {q_4} = - {4.10^{ - 6}}C\) giống nhau đặt tại 4 đỉnh của hình vuông ABCD cạnh 10cm theo thứ tự A, B, C, D. Tìm lực điện tác dụng lên \({q_0} = - {2.10^{ - 6}}C\) đặt tại tâm O của hình vuông.
Biểu diễn các lực tác dụng lên q0 như hình vẽ:
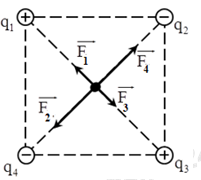
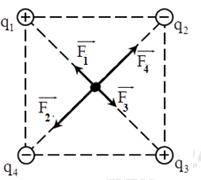
Lực tổng hợp tác dụng lên q0: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} \)
Lực tương tác giữa hai điện tích được xác định bởi công thức: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right|\\OA = OB = OC = OD\end{array} \right. \Rightarrow {F_1} = {F_2} = {F_3} = {F_4}\)
Mặt khác: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}} \uparrow \downarrow \overrightarrow {{F_3}} \Rightarrow {F_{13}} = \left| {{F_1} - {F_3}} \right| = 0\\\overrightarrow {{F_2}} \uparrow \downarrow \overrightarrow {{F_4}} \Rightarrow {F_{24}} = \left| {{F_2} - {F_4}} \right| = 0\end{array} \right. \Rightarrow \overrightarrow F = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{24}}} = 0\)
Cho 4 điện tích \({q_{1\;}} = {q_{2\;}} = {q_{3\;}} = {q_4} = - {2.10^{ - 8}}C\) lần lượt đặt tại 4 đỉnh của hình vuông ABCD cạnh 4cm theo thứ tự A, B, C, D. Tìm lực điện tổng hợp tác dụng lên điện tích đặt tại D?
Biểu diễn các lực tác dụng lên q4 như hình vẽ:
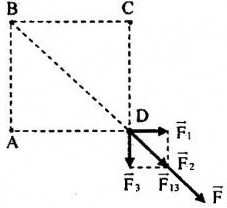
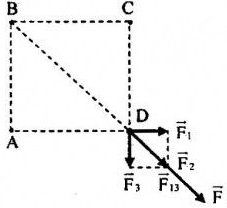
Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right| = {2.10^{ - 8}}C\\AB = BC = CD = DA = 4cm\\BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 cm\end{array} \right. \Rightarrow {F_1} = {F_3}\)
Lực tác dụng lên q4: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \)
Với: \(\left\{ \begin{array}{l}{F_1} = {F_3} = \dfrac{{k.\left| {{q_1}{q_4}} \right|}}{{A{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {{{4.10}^{ - 2}}} \right)}^2}}} = 2,{25.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_4}} \right|}}{{B{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {4\sqrt 2 {{.10}^{ - 2}}} \right)}^2}}} = 1,{125.10^{ - 3}}N\end{array} \right.\)
Ta có: \(\overrightarrow {{F_{13}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_3}} \)
Vì \(\overrightarrow {{F_1}} \bot \overrightarrow {{F_3}} \Rightarrow {F_{13}} = \sqrt {F_1^2 + F_3^2} = {F_1}\sqrt 2 = 2,25\sqrt 2 {.10^{ - 3}}N\)
Ta có: \(\overrightarrow F = \overrightarrow {{F_2}} + \overrightarrow {{F_{13}}} \)
Mà \(\overrightarrow {{F_2}} \uparrow \uparrow \overrightarrow {{F_{13}}} \Rightarrow F = {F_2} + {F_{23}} = 4,{31.10^{ - 3}}N\)

