I. Tích có hướng của hai véc tơ
- Định nghĩa: Cho các véc tơ \(\overrightarrow {{u_1}} = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow {{u_2}} = \left( {{x_2};{y_2};{z_2}} \right)\). Tích có hướng của hai véc tơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) là véc tơ \(\overrightarrow u \), kí hiệu \(\overrightarrow u = \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]\) hoặc $\overrightarrow u = \overrightarrow {{u_1}} \wedge \overrightarrow {{u_2}} $ và được xác định bằng tọa độ như sau:
\(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] =\) \( \left( {\left| {\begin{array}{*{20}{c}}\begin{array}{l}{y_1}\\{y_2}\end{array}&\begin{array}{l}{z_1}\\{z_2}\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l}{z_1}\\{z_2}\end{array}&\begin{array}{l}{x_1}\\{x_2}\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l}{x_1}\\{x_2}\end{array}&\begin{array}{l}{y_1}\\{y_2}\end{array}\end{array}} \right|} \right) =\) \( \left( {{y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1}} \right)\)
Véc tơ \(\overrightarrow u \) vuông góc với cả hai véc tơ \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \)
- Tính chất:
+) \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = - \left[ {\overrightarrow {{u_2}} ;\overrightarrow {{u_1}} } \right]\)
+) \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = \overrightarrow 0 \Leftrightarrow \overrightarrow {{u_1}} \) cùng phương \(\overrightarrow {{u_2}} \)
+) \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] \bot \overrightarrow {{u_1}} ;\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] \bot \overrightarrow {{u_2}} \)
+) \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {{u_3}} = 0 \Leftrightarrow \) ba véc tơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} ,\overrightarrow {{u_3}} \) đồng phẳng.
+) \(\left| {\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right]} \right| = \left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|\sin \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)\)
II. Ứng dụng tích có hướng
- Diện tích tam giác:
\({S_{ABC}} = \dfrac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right|\)
- Diện tích hình bình hành:
\({S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right| = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right|\)
- Thể tích tứ diện:
\({V_{ABCD}} = \dfrac{1}{6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right|\)
- Thể tích khối hộp:
\({V_{ABCD.A'B'C'D'}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right].\overrightarrow {AA'} } \right|\)
Chú ý: Khi thực hành tính toán, các em có thể tính tích có hướng ở ngoài nháp như sau:
+B1: Viết tọa độ mỗi véc tơ hai lần liền nhau, các tọa độ tương ứng của hai véc tơ thẳng cột.
\(\begin{array}{*{20}{r}}{{x_1}}&{{y_1}}&{{z_1}}&{{x_1}}&{{y_1}}&{{z_1}}\\{{x_2}}&{{y_2}}&{{z_2}}&{{x_2}}&{{y_2}}&{{z_2}}\end{array}\)
+ B2: Xóa bỏ hai cột ngoài cùng.
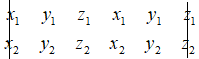
+ B3: Tính toán theo quy luật: Nhân chéo rồi trừ.
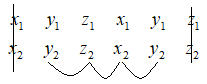
Ví dụ: Cho hai véc tơ \(\overrightarrow u = \left( {1;5;3} \right)\) và \(\overrightarrow v = \left( {2; - 1;0} \right)\). Tính tích có hướng của hai véc tơ trên.
Giải:
Ta sẽ sử dụng phương pháp thực hành ở trên như sau: (chỉ viết ngoài nháp)
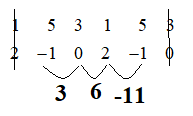
Vậy \(\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {3;6; - 11} \right)\).

