Đề thi thử môn Toán ĐGTD Đại học Bách Khoa - Lần 2

Trong không gian với hệ trục Oxyz, cho $d:\dfrac{{x - 4{m^2}}}{2} = \dfrac{{y + 2m}}{{ - 2}} = \dfrac{{z + 2}}{1}$ và $A\left( { - 1;2;1} \right),B\left( {1; - 2;0} \right)$. Gọi C, D lần lượt là hình chiếu vuông góc của A, B lên d. biết khối tứ diện ABCD có thể tích nhỏ nhất. khẳng định nào dưới đây đúng?

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn$\int {f\left( {\dfrac{1}{2}x} \right)dx}  = {x^2} + 4x + C$ và $\int {f\left( {x - 2} \right)dx}  = a{x^2} + bx + C,a,b \in \mathbb{R}$. Tổng $2a + b$ bằng

Gọi ${z_1}$ và ${z_2}$ là hai nghiệm phức của phương trình ${z^2} - 6z + 25 = 0$. Giá trị của biểu thức $P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}$ là

Cho lăng trụ tam giác đếu ABC.A’B’C’ có thể tích bằng 1. Gọi (T) là hình trụ nội tiếp lăng trụ và M là tâm của mặt bên BCC’B’. Mặt phẳng (P) chứa AM cắt hình trụ (T) như hình vẽ.

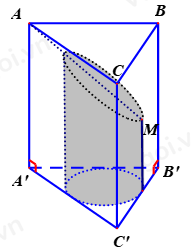
Thể tích khối hình còn lại (phần tô đậm) của khối trụ (T) là

Cho hàm số $y = f\left( x \right)$. Hàm số $y = f'\left( x \right)$ có bảng biến thiên như sau

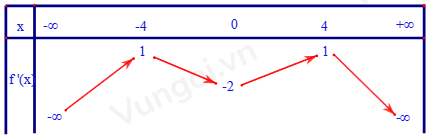
Số điểm cực trị của hàm số $y = f\left( {{{\left( {{x^4} + 3{x^2} + 2} \right)}^2}} \right) + \left( {{x^4} + 3{x^2} + 1} \right)\left( {{x^4} + 3{x^2} + 3} \right)$ là

Tích tất cả các nghiệm của phương trình $2{\left( {{{\log }_4}x} \right)^2} - 3{\log _4}x - 2 = 0$

Có bao nhiêu giá trị nguyên của tham số m để tập nghiệm của bất phương trình ${\log _2}\left( {{x^2} + 2x + m} \right) - 2{\log _2}\left( {2x - 1} \right) > 0$ chứa đúng hai số nguyên?

Cho khai triển ${\left( {2 + 3x} \right)^{2021}} = {a_0} + {a_1}x + {a_2}{x^2}... + {a_{2021}}{x^{2021}}$. Hệ số lớn nhất trong khai triển đã cho là

Cho hình trụ có đường kính đáy bằng 2a. thiết diện qua trục của hình trụ là hình chữ nhật có đường chéo là 3a. diện tích toàn phần của hình trụ là

Hàm số $y = \dfrac{{{x^2} - 3mx + 4}}{{x - m}}$ không có cực trị khi và chỉ khi

Tổng tất cả các giá trị nguyên của m để phương trình ${25^{x + 1}} - {5^{x + 2}} - 4m = 0$ có nghiệm x<1 là

Một bình đựng 35 quả cầu phân biệt, trong đó có 2 quả cầu màu xanh và 15 quả cầu màu đỏ. Chọn ngẫu nhiên 5 quả cầu xác suất để trong 5 quả cầu được chọn có cả quả cầu màu xanh và quả cầu màu đỏ là

Cho hình chóp S.ABCD có $SA \bot \left( {ABCD} \right)$, $SA = a$ và đáy ABCD là hình vuông cạnh 2a. kẻ $AH \bot SC,H \in SC$. Khoảng cách từ H đến mặt phẳng (ABCD) bằng

Cho hàm số $y = f\left( x \right)$ có đồ thị trên $\left[ { - 1;3} \right]$ như hình vẽ

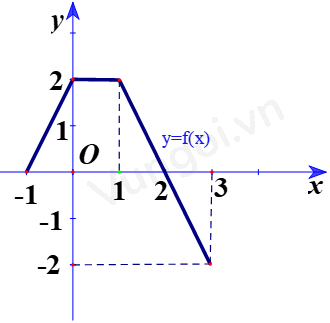
Khi đó $\int\limits_{ - 1}^3 {f\left( x \right)dx}$

Tập hợp tất cả các giá trị của m để hàm số $y =  - {x^3} + 2m{x^2} - \left( {m + \dfrac{1}{3}} \right)x - 4$ nghịch biến trên $\mathbb{R}$ là

Tại Hà Nội, giá nước sinh hoạt được tính như bảng sau (Đơn vị tính: đồng/${m^3}$)

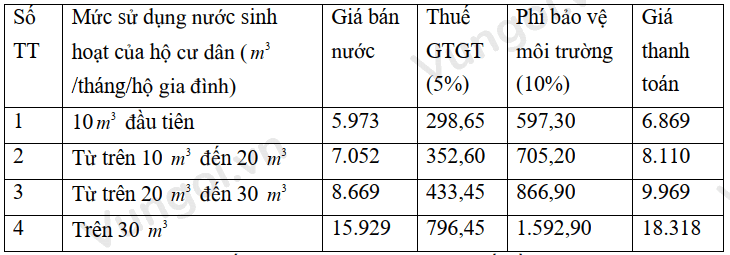
Một hộ gia đình tiêu thụ hết 40 ${m^3}$ nước một tháng thì số tiền phải trả là

Số các số tự nhiên có bốn chữ số $\overline {abcd}$ thoả mãn $a \le b \le c \le d$ là

Cho hình cầu bán kính bằng $2a$. Thể tích lớn nhất của khối trụ nội tiếp trong hình cầu đã cho là:

Xét các số phức $x$ thỏa mãn $|z - 2| = |z - 2i|$. Môđun nhỏ nhất của số phức $w = z + 4 - 2i$ bằng

Trong không gian với hệ trục tọa độ vuông góc Oxyz cho hai đưòng thẳng ${d_1}:\dfrac{{x + 2}}{3} = \dfrac{{y + 5}}{6} = \dfrac{{z + 1}}{2}$ và ${d_2}:\dfrac{{x + 1}}{2} = \dfrac{y}{1} = \dfrac{{z + 1}}{2}$. Phương trình đường thẳng phân giác của góc nhọn tạo bởi ${d_1}$ và ${d_2}$ là

Một nhà máy sản xuất bia xây dựng một hệ thống gồm các dây chuyền rửa vỏ chai bia tự động được giám sát và vận hành bởi một công nhân vởi chi phí là 14 Euro/giờ. Mỗi dây chuyền trong một giờ có thể sục rửa được 350 vỏ chai bia và chi phí cài đặt một dây chuyền là 48 Euro. Mỗi đợt, hệ thông cần sục rửa 30000 vỏ chai bia thì để tốn ít chi phi nhất, nhà máy cần sử dụng số dây chuyền là

Cho hàm số $y = {x^3} - (2m + 1){x^2}$$+ \left( {{m^2} - m + 3} \right)x$$+ 2{m^2} - 3m$

Số giá trị nguyên của $m$ thuộc $( - 20;10)$ để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là

Trong không gian Oxyz cho điểm $I(2;0;1)$ và đường thẳng $d:\dfrac{x}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{{ - 2}}$. Phương trình mặt cầu tâm $I$ và tiếp xúc với d là

Cho hình chóp tứ giác đều $S.ABCD$ có $AB = 2a,SA = a\sqrt 5$. Khoảng cách từ đường thẳng $AB$ đến $(SCD)$ bằng

Cho một dãy số có các số hạng đầu tiên là $1,6,16,31,51$. Biết rằng hiệu của hai số hạng liên tiếp của dãy số đó lập thành một cấp số cộng: $5,10,15,20, \ldots ,5n$. Số 6126 là số hạng thứ bao nhiêu của dãy số đã cho?

Một chiếc xe cứu hộ xuất phát từ góc của một hồ nước hình chữ nhật có các cạnh dài $1600\;{\rm{m}}$ và rộng $600\;{\rm{m}}$. Xe vừa có thể đi trên bờ hồ và đi trên mặt nước với vận tốc tương ứng là $20\;{\rm{m}}/{\rm{s}}$ và $12\;{\rm{m}}/{\rm{s}}$. Tính thời gian xe đi nhanh nhất đến tâm của hồ.

Tính góc giữa hai đường thẳng $SA$và $AB$.

Biết tổng khối lượng của các cạnh của  và 9 bóng đèn là $5\;{\rm{kg}}$, bỏ qua khối lượng của các dây $AB,{\rm{ }}AC,{\rm{ }}AD$. Tính lực căng trên dây $AB$.