Đề thi Toán học - Đề số 2

Số tiệm cận ngang của đồ thị hàm số \(y = 2x - 1 + \sqrt {4{x^2} - 4} \) là

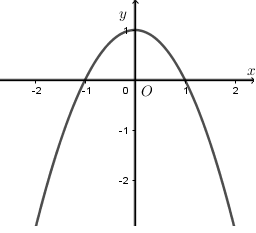
Gọi $S$ là diện tích của Ban Công của một ngôi nhà có dạng như hình vẽ ($S$ được giới hạn bởi parabol $\left( P \right)$  và trục $Ox$). Giá trị của S là:

Một thiết bị trong năm 2021 được định giá 100 triệu đồng. Trong 5 năm tiếp theo, mỗi năm giá trị thiết bị giảm 6 % so với năm trước và từ năm thứ 6 trở đi, mỗi năm giá trị thiết bị giảm 10 % so với  năm trước. Hỏi bắt đầu từ năm nào thì giá trị thiết bị nhỏ hơn 50 triệu đồng?

Trong không gian với hệ tọa độ $Oxyz$, cho ba vectơ $\vec a = \left( {1;m;2} \right),\vec b = \left( {m + 1;2;1} \right)$ và \(\vec c = \left( {0;m - 2;2} \right)\). Giá trị \(m\) bằng bao nhiêu để ba vectơ \(\vec a,\vec b,\vec c\) đồng phẳng

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 4,{\rm{ }}AD = 3.\) Mặt phẳng \((ACD')\) tạo với mặt đáy một góc \({60^ \circ }.\) Tính khoảng cách giữa hai mặt đáy của hình hộp.

Một nhóm $4$ đường thẳng song song cắt một nhóm $5$ đường thẳng song song khác. Hỏi có bao nhiêu hình bình hành được tạo thành?

Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón có bán kính bằng nhau; biết rằng nếu kem tan chảy hết thì sẽ làm đầy phần ốc quế. Biết thể tích phần kem sau khi tan chảy chỉ bằng $75\% $ thể tích kem đóng băng ban đầu. Gọi $h$ và $r$ lần lượt là chiều cao và bán kính của phần ốc quế. Tính tỉ số \(\dfrac{h}{r}\).

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = {\sin ^2}x + 3\sin 2x + 3{\cos ^2}x\):

Bạn Bách thả 1 quả bóng cao su từ độ cao 12m so với mặt đất. Mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng \(\dfrac{2}{3}\) độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng số quãng đường quả bóng đã di chuyển (từ lúc thả bóng cho tới khi quả bóng không nảy nữa) gần nhất với kết quả nào sau đây?

Cho các số phức \({z_1} = 3 - 2i,\) \({z_2} = 1 + 4i\) và \({z_3} =  - 1 + i\) có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm \(A,B,C\). Diện tích tam giác ABC bằng:

Cho ba điểm $A,B,C$ lần lượt biểu diễn các số phức sau \({z_1} = 1 + i;\,{z_2} = {z_1}^2;\,{z_3} = m - i\). Tìm các giá trị thực của $m$ sao cho tam giác $ABC$ vuông tại $B$.

Cho các chữ số 0,1,2,3,4,5,6. Gọi \(S\) là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ các chữ số đã cho. Lấy ngẫu nhiên 2 số từ \(S\), gọi \(A\) là biến cố: “tổng hai số lấy được là một số chẵn”. Xác suất của biến cố \(A\) là:

Một quần thể sinh vật tại thời điểm hiện tại có \(T\) (con), biết quần thể đó có tỉ lệ tăng trưởng \(r\) theo năm, hỏi số sinh vật trong quần thể từ \(2\) năm trước là bao nhiêu?

Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\dfrac{1}{3}} \right)^{x - 2}}\)

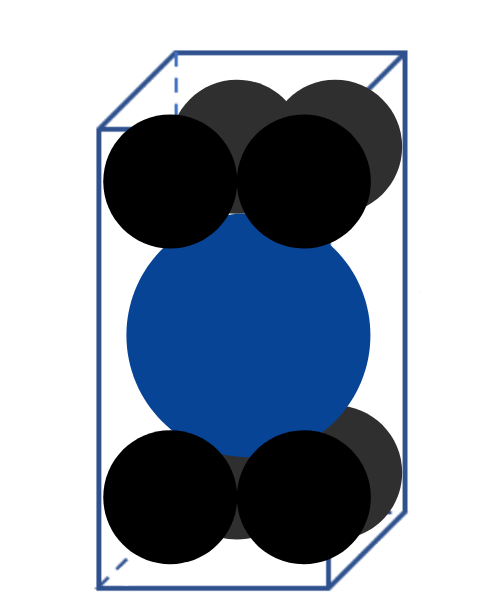
Cho một hình hộp chữ nhật kích thước $4 \times 4 \times h$ chứa một khối cầu lớn có bán kính bằng 2 và 8 khối cầu nhỏ có bán kính bằng 1. Biết rằng các khối cầu đều tiếp xúc với nhau và tiếp xúc với các mặt của hình hộp (tham khảo hình vẽ). Thể tích của khối hộp bằng

Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng \(a\sqrt 2 \). Khoảng cách từ điểm \(S\) đến mặt phẳng (ABCD) bằng

Phương trình \({\sin ^2}3x + \left( {{m^2} - 3} \right)\sin 3x + {m^2} - 4 = 0\) khi \(m = 1\) có nghiệm là:

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm\(A(1;1;1),B( - 1; - 1;0)\) và \(C(3;1; - 1)\). Tìm tọa độ điểm $M$ thuộc $\left( {Oxy} \right)$  và cách đều các điểm \(A,B,C\) .

Một chất điểm đang chuyển động với vận tốc \({v_0} = 15\;{\rm{m/s}}\) thì tăng tốc với gia tốc \(a\left( t \right) = {t^2} + 4t\;\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\). Tính quãng đường chất điểm đó đi được trong khoảng thời gian \(3\) giây kể từ lúc bắt đầu tăng vận tốc.

Cho hình nón có góc ở đỉnh bằng \({120^0}\) và đường cao bằng \(2.\) Tính diện tích xung quanh của hình nón đã cho.

Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ lần lượt có phương trình $x + 2y - 2z + 1 = 0$ và $x - 2y + 2z - 1 = 0$. Gọi $\left( S \right)$ là quỹ tích các điểm cách đều hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.  Tìm khẳng định đúng.

Cho hàm số \(f\left( x \right)\) có đồ thị trên đoạn \(\left[ { - 3;3} \right]\) là đường gấp khúc ABCD như hình vẽ.

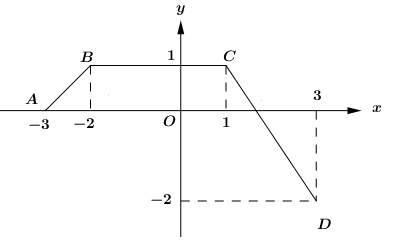
Tính \(\int\limits_{ - 3}^3 {f\left( x \right)dx} \).

Gọi $x_1, x_2$ là các nghiệm của phương trình ${\left( {{{\log }_{\frac{1}{3}}}x} \right)^2} - \left( {\sqrt 3  + 1} \right){\log _3}x + \sqrt 3  = 0$. Khi đó tích $x_1, x_2$ bằng:

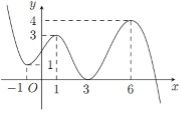
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Tìm số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\).

Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích \(V\). Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao cho \(MB = 2MB'\). Mặt phẳng \(\left( \alpha  \right)\) đi qua \(M\) và vuông góc với \(AC'\) cắt các cạnh \(DD'\), \(DC\), \(BC\) lần lượt tại \(N\), \(P\), \(Q\). Gọi \({V_1}\) là thể tích của khối đa diện \(CPQMNC'\).Tính tỉ số \(\dfrac{{{V_1}}}{V}\).

Vị trí đạn bay cao nhất cách mặt đất bao nhiêu?

Máy bắn đá cách tường thành địch \(90\;{\rm{m}}\). Biết tường thành cao \(30\;{\rm{m}}\). Hỏi chiều cao khi đạn bay đến tường thành thì cao hơn hay thấp hơn tường thành bao nhiêu mét?

Địch xây chòi phòng thủ cao \(20\;{\rm{m}}\) phía trước tường thành. Hỏi phải đặt máy bắn đá cách chòi bao xa để đạn có thể bắn trúng chòi? Biết rằng để tránh bị địch tấn công thì máy bắn đá phải đặt cách thành địch ít nhất \(50\;{\rm{m}}\).

Tìm số hạng tổng quát của dãy số \(\left( {{u_n}} \right)\).

Số hạng \({u_k} = 100006\) là số hạng thứ bao nhiêu của dãy?

Tính tổng 100 số hạng đầu tiên của dãy.