Câu hỏi:
3 năm trước
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng \(a\sqrt 2 \). Khoảng cách từ điểm \(S\) đến mặt phẳng (ABCD) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
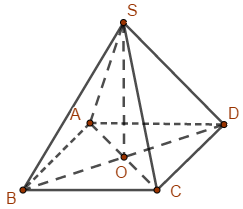
Bước 1:
Gọi O là giao điểm của AC và BD.
S.ABCD là hình chóp đều nên O là hình chiếu của S lên (ABCD).
=> \(d\left( {S,\left( {ABCD} \right)} \right) = SO\)
Bước 2:
ABCD là hình vuông nên
\(\begin{array}{l}AC = a\sqrt 2 .\sqrt 2 = 2a = > AO = a\\ = > S{O^2} = S{A^2} - A{O^2} = 2{a^2} - {a^2} = {a^2}\\ = > SO = a\end{array}\)
Hướng dẫn giải:
Bước 1: Xác định hình chiếu của S lên (ABCD) từ đó tìm ra khoảng cách từ S đến (ABCD).
Bước 2: Tính khoảng cách.
Giải thích thêm:
Hình chóp đều có đáy là hình vuông và hình chiếu của S đến (ABCD) là tâm của đáy.