Kết quả:
0/30
Thời gian làm bài: 00:00:00
Đồ thị hàm số nào sau đây có 3 đường tiệm cận?
Bác Năm làm một cái cửa nhà hình parabol bằng gỗ có chiều cao từ mặt đất đến đỉnh là \(2,25\) mét, chiều rộng tiếp giáp với mặt đất là \(3\) mét. Giá tiền mỗi mét vuông gỗ là \(1500000\) đồng. Vậy số tiền bác Năm phải trả là:
Một người vay ngân hàng một số tiền với lãi suất mỗi tháng là $1,12\% $. Biết cuối mỗi tháng người đó phải trả cho ngân hàng $3.000.000$ đồng và trả trong $1$ năm thì hết nợ. Số tiền người đó vay là:
Diện tích hình bình hành \(ABCD\) có các điểm \(A\left( {1;0;0} \right),B\left( {0;1;2} \right),C\left( { - 1;0;0} \right)\) là:
Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a.$ Khoảng cách giữa $\left( {AB'C} \right)$ và $\left( {A'DC'} \right)$ bằng:
Có bao nhiêu cách sắp xếp $8$ viên bi đỏ khác nhau và $8$ viên bi đen khác nhau thành một dãy sao cho hai viên bi cùng màu không được ở cạnh nhau?
Một hình nón có bán kính đáy bằng $1$, chiều cao nón bằng $2$. Khi đó góc ở đỉnh của nón là $2\varphi $ thỏa mãn
Phương trình \(\cot 20x = 1\) có bao nhiêu nghiệm thuộc khoảng \(\left[ { - 50\pi ;0} \right]\)?
Tìm số hữu tỉ biểu diễn số $0,111111 \ldots$. chu kỳ (1).
Cho các số phức \({z_1} = 2,{z_2} = - 4i,{z_3} = 2 - 4i\) có điểm biểu diễn tương ứng trên mặt phẳng tọa độ Oxy là A, B, C. Diện tích tam giác ABC bằng
Tập điểm biểu diễn số phức $z$ thỏa mãn ${\left| z \right|^2} = {z^2}$ là:
Gọi \(S\) là tập hợp tất cả các số tự nhiên có \(4\) chữ số đôi một khác nhau và các chữ số thuộc tập hợp \(\left\{ {1,2,3,4,5,6,7} \right\}\). Chọn ngẫu nhiên một số thuộc \(S\), xác suất để số đó không có hai chữ số liên tiếp nào cùng chẵn bằng
Sự tăng trưởng của 1 loài vi khuẩn được tính theo công thức $S = A.{e^{rt}}$ , trong đó $A$ là số lượng vi khuẩn ban đầu, $r$ là tỉ lệ tăng trưởng $(r>0)$, $t$ là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là $150$ con và sau $5$ giờ có $450$ con, tìm số lượng vi khuẩn sau 10 giờ tăng trưởng.
Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{5}} \right)^{{x^2} - 2x}} \ge \dfrac{1}{{125}}\)
Cho lăng trụ đứng ABC.A'B'C' có chiều cao bằng 4, đáy ABC là tam giác cân tại A với AB = AC = 2; \(\angle BAC = {120^0}\). Tính diện tích mặt cầu ngoại tiếp lăng trụ trên.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$; góc giữa đường thẳng $SB$ và mặt phẳng $\left( {ABC} \right)$ bằng ${60^0}$. Gọi $M$ là trung điểm của cạnh $AB$. Tính khoảng cách \(d\) từ $B$ đến mặt phẳng $\left( {SMC} \right)$.
Phương trình \(3\sin 3x + \sqrt 3 \cos 9x = 1 + 4{\sin ^3}3x\) là:
Trong không gian $Oxyz$ cho $3$ véc tơ: \(\vec a\left( {4;2;5} \right),\vec b\left( {3;1;3} \right),\vec c\left( {2;0;1} \right)\). Kết luận nào sau đây đúng
Một ô tô đang đứng và bắt đầu chuyển động theo một đường thẳng với gia tốc \(a\left( t \right) = 6 - 3t\,\,\left( {m/{s^2}} \right)\), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động. Hỏi quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là:
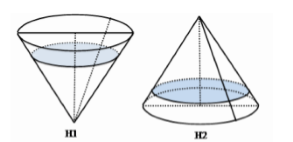
Một khối đồ chơi có dạng khối nón, chiều cao bằng \(20cm\), trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình H1 thì chiều cao của lượng nước bằng \(\dfrac{2}{3}\) chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo hình H2 thì chiều cao \(h\) của lượng nước trong khối đó gần với giá trị nào sau đây?
Trong không gian \(Oxyz\), cho mặt cầu \(\left( C \right):\,\,\,{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 1\) và hai điểm \(A\left( {2;1;0} \right)\), \(B\left( {0;2;0} \right)\). Khi điểm \(S\) thay đổi trên mặt cầu \(\left( C \right)\), thể tích của khối chóp \(S.OAB\) có giá trị lớn nhất bằng bao nhiêu?
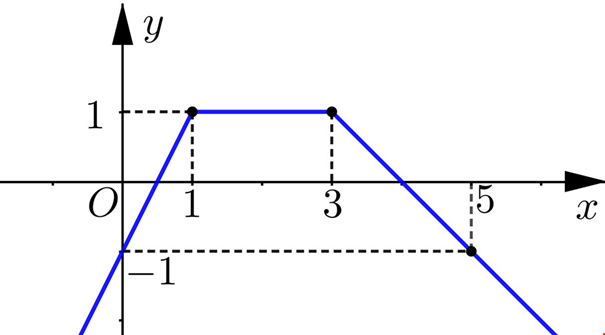
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên đoạn [0;5] là đường gấp khúc như hình vẽ. Tính tích phân \(\int\limits_0^5 {\left[ {2f\left( x \right) - 1} \right]dx} \)
Tìm tất cả các giá trị thực của $m$ để phương trình \(2{\log _2}\left| x \right| + {\log _2}\left| {x + 3} \right| = m\) có $3$ nghiệm thực phân biệt.
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
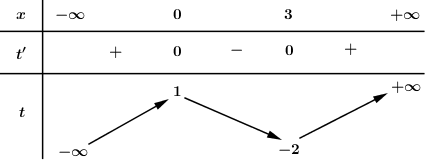
Số điểm cực trị của hàm số \(f\left( {{x^2} - 2x} \right)\) là:
Cho tứ diện \(ABCD\) có \(G\) là điểm thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Mặt phẳng thay đổi chứa \(BG\) và cắt \(AC,\,\,AD\) lần lượt tại \(M\) và \(N\). Giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}}\) là
Tính góc giữa hai mặt phẳng $\left(A B B^{\prime} A^{\prime}\right)$ và $(A B C)$
Tính thể tích khối lăng trụ $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$
Thiết lập công thức liên hệ giữa quãng đường di chuyển và số tiền tương ứng phải trả. Nếu một người đi taxi của hãng $\mathrm{X}$ phải trả số tiền xe là $475000 \mathrm{VNĐ}$ thì người đó đã đi quãng đường là bao nhiêu?
Một người đi taxi của hãng $\mathrm{X}$ từ $A$ đến $B$, sau đó phải bắt taxi một lần nữa để đi từ $B$ đến $C$. Biết quãng đường $A B$ trong khoảng từ 10 đến $40 \mathrm{~km}$, quãng đường $B C$ dài hơn quãng đường $A B$ là $32 \mathrm{~km}$. Số tiền người đó phải trả ở quãng đường $B C$ gấp 2,8 lần số tiền phải trả ở quãng đường $A B$. Tính độ dài quãng đường $A B$
Ngày Valentine, hãng $X$ áp dụng chương trình giảm giá $10 \%$ cho khách hàng, tối đa $50000$VNĐ. Một người đi taxi của hãng $\mathrm{X}$ trong dịp này phải trả $360000$VNĐ thì người đó đã đi quãng đường là bao nhiêu?

