Câu hỏi:
2 năm trước
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa (AB′C) và (A′DC′) bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
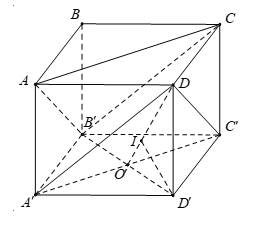
Ta có: {A′C′//ACDC′//AB′⇒(A′C′D)//(ACB′)
Gọi O′ là tâm của hình vuông A′B′C′D′.
Ta có d((AB′C),(A′DC′))=d(B′,(A′DC′))=d(D′,(A′DC′))
Gọi I là hình chiếu của D′ trên O′D.
Vì D′O′⊥A′C′,DO′⊥A′C′ nên A′C′⊥(DOD′)⇒A′C′⊥D′I.
Mà D′I⊥DO′ nên I là hình chiếu của D′ trên (A′DC′).
⇒d((AB′C),(A′DC′))=d(D′,(A′DC′))=D′I=D′O′.D′D√D′O′2+D′D2=a√22.a√(a√22)2+a2=a√33.
Hướng dẫn giải:
- Chứng minh hai mặt phẳng (AB′C) và (A′DC′) song song.
- Khoảng cách cần tìm chính là khoảng cách từ B′ đến mặt phẳng (A′C′D).
- Tính khoảng cách d(B′,(A′DC′)) bằng phương pháp tỉ lệ khoảng cách.

