Đề thi chính thức ĐGTD Bách khoa 2022 - mã 103
Kỳ thi ĐGTD ĐH Bách Khoa
Kết quả:
0/25
Thời gian làm bài: 00:00:00
Đề thi chính thức ĐGTD Bách khoa 2022
Cho số thực \(a\) sao cho \(f\left( x \right) = \left\{ \begin{array}{l}ax + 4\,\,{\rm{ khi }}\,x \ne - 1\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{ khi }}\,x = - 1\end{array} \right.\) liên tục trên \(\mathbb{R}\). Khi đó, \(a\) bằng
Đề thi chính thức ĐGTD Bách khoa 2022
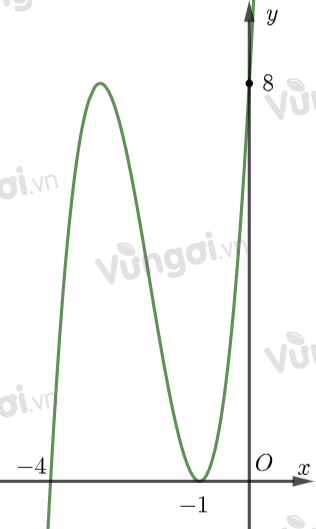
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \(\left( {a,b,c,d \in \mathbb{R}} \right)\) có đồ thị như hình bên. Khi đó, \(a + b - c - d\) bằng
Đề thi chính thức ĐGTD Bách khoa 2022
Cho hai hàm số f(x) và g(x) liên tục trên R. Khẳng định nào dưới đây là sai?
Đề thi chính thức ĐGTD Bách khoa 2022
Với hai số thực \(a\) và \(b\) thỏa mãn \(a < b\), đặt \(M = \int\limits_a^b {\left( { - 3 + 4x - {x^2}} \right)dx} \). Khi M đạt giá trị lớn nhất thì
Đề thi chính thức ĐGTD Bách khoa 2022
Cho hai số thực dương a,b thỏa mãn \(\sqrt[4]{{\log a}} + \sqrt {\log b} + \log \sqrt[4]{a} + \log \sqrt b = 108\) và bốn số \(\sqrt[4]{{\log a}},\sqrt {\log b} ,\log \sqrt[4]{a},\log \sqrt b \) là các số nguyên dương. Khi đó, ab bằng
Đề thi chính thức ĐGTD Bách khoa 2022
Trong không gian cho mặt cầu tâm I và 10 đường thẳng phân biệt đi qua điểm I cắt mặt cầu tại 20 điểm. Gọi S là tập hợp các hình chữ nhật tâm I và có các định là bốn điểm trong 20 điểm trên. Số phần tử của S là
Đề thi chính thức ĐGTD Bách khoa 2022
Biết hai số thực a,b thoả mãn \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {16{x^2} + ax + 2022} - bx} \right) = - 3\). Khi đó, khẳng định nào dưới đây đúng?
Đề thi chính thức ĐGTD Bách khoa 2022
Cho một khối trụ tròn xoay và tam giác ABC vuông cân tại A, trong đó A, B nằm trên đường tròn đáy của khối trụ và C nằm trên đường tròn đáy còn lại. Biết \(AB = a\), mặt phẳng \(\left( {ABC} \right)\) tạo với mặt phẳng đáy của khối trụ một góc bằng \({45^o}\). Thể tích khối trụ đã cho bằng
Đề thi chính thức ĐGTD Bách khoa 2022
Cho số phức \(z\) thỏa mãn \(\left| {z - 3} \right| = \left| {z + 2i} \right|\). Tập hợp điểm biểu diễn của các số phức \(w = \left( {i + 1} \right)z\) là một đường thẳng có phương trình
Đề thi chính thức ĐGTD Bách khoa 2022
Khẳng định nào dưới đây đúng?
Đề thi chính thức ĐGTD Bách khoa 2022
Khẳng định nào dưới đây đúng?
Đề thi chính thức ĐGTD Bách khoa 2022
Số nghiệm \(x \in \left[ {0;2022\pi } \right]\) của phương trình \(2\cos x-\cos 2x = 1\) là
Đề thi chính thức ĐGTD Bách khoa 2022
Trong không gian \(Ozyz\), cho hai điểm \(A\left( {2;1;0} \right)\) và \(B\left( {0;4;0} \right).\) Xét điểm S thay đổi luôn thuộc trục \(Oz\), gọi \(K\) là trung điểm của \(SB,H\) là hình chiếu vuông góc của \(O\) trên \(AK\). Biết rằng \(H\) luôn thuộc một đường tròn cố định, chu vi của đường tròn đó là
Đề thi chính thức ĐGTD Bách khoa 2022
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {\left( { - 1} \right)^n}\dfrac{{2022n}}{{n + 1}},\,n \in {\mathbb{N}^*}\). Khẳng định nào dưới đây đúng?
Đề thi chính thức ĐGTD Bách khoa 2022
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(a\) và cạnh bên tạo với đáy một góc \({45^o}\). Gọi M,N lần lượt là trung điểm các cạnh SB,SD. Khoảng cách giữa hai đường thẳng MN và BC bằng
Đề thi chính thức ĐGTD Bách khoa 2022
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1;1;1} \right),{\rm{ }}B\left( { - 1;1;0} \right),{\rm{ }}C\left( {3;1; - 1} \right).\) Gọi \(M\left( {a;b;c} \right)\) là điểm thuộc mặt phẳng \(\left( {Oxz} \right)\) và cách đều ba điểm \(A,B,C\). Khi đó, \(a + b - c\) bằng
Đề thi chính thức ĐGTD Bách khoa 2022
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa đường thẳng $B'C$ và mặt phẳng \(\left( {BDD'B'} \right)\) bằng
Đề thi chính thức ĐGTD Bách khoa 2022
Gọi A là tập hợp các số tự nhiên có bốn chữ số khác nhau lập từ các chữ số 0,1,2,3,4,5. Chọn ngẫu nhiên một số từ A. Xác suất để số chọn ra có hai chữ số chẵn, hai chữ số lẻ bằng
Đề thi chính thức ĐGTD Bách khoa 2022
Hàm số nào dưới đây tuần hoàn với chu kì \(\pi \)?
Đề thi chính thức ĐGTD Bách khoa 2022
Khẳng định nào dưới đây đúng?
Đề thi chính thức ĐGTD Bách khoa 2022
Biết phương trình \({z^3} + a{z^2} + 6z + b = 0\left( {a,b \in \mathbb{R}} \right)\) có 3 nghiệm \({z_1},{z_2},{z_3}\) trong đó \({z_1} = 5 + i\). Khi đó, \({\left| {{z_2}} \right|^2} + {\left| {{z_3}} \right|^2}\) bằng
Đề thi chính thức ĐGTD Bách khoa 2022
Cho hàm số \(y = {\rm{ }}f\left( x \right)\) xác định trên khoảng \(\left( {a;b} \right)\) và \({x_o} \in \left( {a;b} \right)\). Khẳng định nào dưới đây đúng?
Đề thi chính thức ĐGTD Bách khoa 2022
Gọi S là tập hợp các số nguyên dương sao cho ba số \({\log _3}x,\,{\log _9}x\) và 3 là độ dài ba cạnh của một tam giác. Khi đó, số phần tử của S là
Đề thi chính thức ĐGTD Bách khoa 2022
Trong mặt phẳng tọa độ \(Oxy\), cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\) và điểm \(A\left( {2;9} \right)\). Đường thẳng \(d:{\rm{ }}2x + ay + b = 0\left( {b > 0,{\rm{ }}a \in R} \right)\) đi qua điểm A và cắt đường tròn \(\left( C \right)\) tại hai điểm B,C. Khi \(BC = 4,{\rm{ }}a-b\) thuộc khoảng nào dưới đây?
Đề thi chính thức ĐGTD Bách khoa 2022
Cho \(b > a > 1\). Đường thẳng \(y = 2\) cắt đồ thị hàm số \(y = {\log _a}x\) và đồ thị hàm số \(y = {\log _b}x\), tại các điểm có hoành độ lần lượt là \({x_1}\) và \({x_2}\). Biết rằng \({x_2} = 8{x_1}\), giá trị của \(\dfrac{b}{a}\) bằng

