Đề thi chính thức ĐGTD Bách khoa 2022
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(a\) và cạnh bên tạo với đáy một góc \({45^o}\). Gọi M,N lần lượt là trung điểm các cạnh SB,SD. Khoảng cách giữa hai đường thẳng MN và BC bằng
Trả lời bởi giáo viên
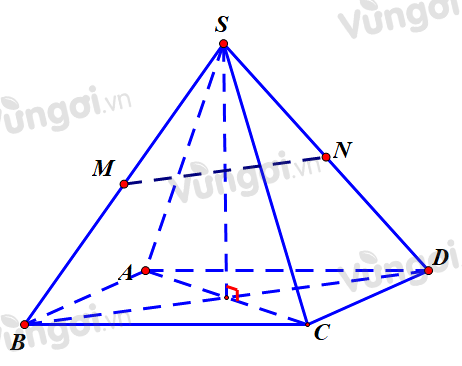
Ta có: \(MN//(ABCD)\)
\(d\left( {MN;BC} \right) = d\left( {MN;\left( {ABCD} \right)} \right) = \dfrac{1}{2}d\left( {S;\left( {ABCD} \right)} \right)\)
Do góc tạo bởi cạnh bên và mặt đáy là \({45^0}\) nên \(\widehat {\left( {SD;\left( {ABCD} \right)} \right)} = {45^0} \Rightarrow \widehat {SBD} = {45^0}\)
\( \Rightarrow \Delta SBD\) vuông cân tại S.
Gọi O là tâm mặt đáy.
\( \Rightarrow SO \bot \left( {ABCD} \right)\)\( \Rightarrow SO \bot BD \Rightarrow SO = \dfrac{{BD}}{2} = \dfrac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {MN;BC} \right) = \dfrac{{a\sqrt 2 }}{4}\)
Hướng dẫn giải:
- Đưa về khoảng cách từ điểm đến mặt phẳng.
- Tính khoảng cách từ S đến (ABCD).