Đề thi chính thức ĐGTD Bách khoa 2022

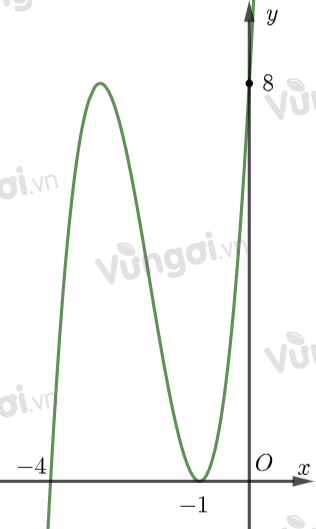
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \(\left( {a,b,c,d \in \mathbb{R}} \right)\) có đồ thị như hình bên. Khi đó, \(a + b - c - d\) bằng

Đề thi chính thức ĐGTD Bách khoa 2022

Cho số thực \(a\) sao cho \(f\left( x \right) = \left\{ \begin{array}{l}ax + 4\,\,{\rm{ khi }}\,x \ne  - 1\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{ khi }}\,x =  - 1\end{array} \right.\) liên tục trên \(\mathbb{R}\). Khi đó, \(a\) bằng

Đề thi chính thức ĐGTD Bách khoa 2022

Cho hai hàm số f(x) và g(x) liên tục trên R. Khẳng định nào dưới đây là sai?

Đề thi chính thức ĐGTD Bách khoa 2022

Với hai số thực \(a\) và \(b\) thỏa mãn \(a < b\), đặt \(M = \int\limits_a^b {\left( { - 3 + 4x - {x^2}} \right)dx} \). Khi M đạt giá trị lớn nhất thì

Đề thi chính thức ĐGTD Bách khoa 2022

Cho hai số thực dương a,b thỏa mãn \(\sqrt[4]{{\log a}} + \sqrt {\log b}  + \log \sqrt[4]{a} + \log \sqrt b  = 108\) và bốn số \(\sqrt[4]{{\log a}},\sqrt {\log b} ,\log \sqrt[4]{a},\log \sqrt b \) là các số nguyên dương. Khi đó, ab bằng

Đề thi chính thức ĐGTD Bách khoa 2022

Trong không gian cho mặt cầu tâm I và 10 đường thẳng phân biệt đi qua điểm I cắt mặt cầu tại 20 điểm. Gọi S là tập hợp các hình chữ nhật tâm I và có các định là bốn điểm trong 20 điểm trên. Số phần tử của S là

Đề thi chính thức ĐGTD Bách khoa 2022

Biết hai số thực a,b thoả mãn \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {16{x^2} + ax + 2022}  - bx} \right) =  - 3\). Khi đó, khẳng định nào dưới đây đúng?