Đề thi chính thức ĐGTD Bách khoa 2022
Trong mặt phẳng tọa độ \(Oxy\), cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\) và điểm \(A\left( {2;9} \right)\). Đường thẳng \(d:{\rm{ }}2x + ay + b = 0\left( {b > 0,{\rm{ }}a \in R} \right)\) đi qua điểm A và cắt đường tròn \(\left( C \right)\) tại hai điểm B,C. Khi \(BC = 4,{\rm{ }}a-b\) thuộc khoảng nào dưới đây?
Trả lời bởi giáo viên
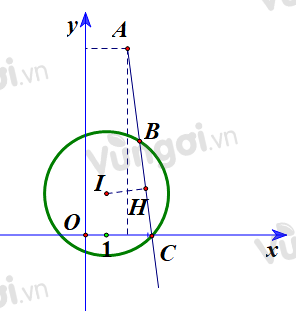
Gọi I, H lần lượt là tâm đường tròn (C ) và hình chiếu của I lên BC.
Ta có:
\(\begin{array}{l}d\left( {I;d} \right) = IH = \sqrt {9 - 4} = \sqrt 5 \\ \Rightarrow \dfrac{{\left| {2.1 + a.2 + b} \right|}}{{\sqrt {4 + {a^2}} }} = \sqrt 5 \\ \Leftrightarrow {\left( {2a + b + 2} \right)^2} = 5.\left( {{a^2} + 4} \right)\left( * \right)\end{array}\)
Vì d đi qua A nên ta có: \(2.2 + a.9 + b = 0 \Leftrightarrow b = - 4 - 9a\). Thay vào phương trình (*) ta được:
\(\begin{array}{l}{\left( { - 2 - 7a} \right)^2} = 5{a^2} + 20\\ \Leftrightarrow 49{a^2} + 28a + 4 = 5{a^2} + 20\\ \Leftrightarrow 44{a^2} + 28a - 16 = 0\\ \Leftrightarrow 11{a^2} + 7a - 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}a = - 1\\a = \dfrac{4}{{11}}\end{array} \right.\end{array}\)
Với \(a = - 1 \Rightarrow b = 9 \Rightarrow a - b = - 10\)(t/m)
Với \(a = \dfrac{4}{{11}} \Rightarrow b = - \dfrac{{80}}{{11}}\left( {ktm} \right)\)
Vậy \(a - b\) thuộc \(\left( { - \infty ; - 8} \right)\)
Hướng dẫn giải:
- Gọi I, H lần lượt là tâm đường tròn (C ) và hình chiếu của I lên BC.
- Sử dụng công thức khoảng cách \(d\left( {I;d} \right) = IH\) để lập phương trình a và b.
- Từ d đi qua A, lập phương trình 2. Giải hệ phương trình tìm b>0. Từ đó tìm a và tính a-b.