Đề thi chính thức ĐGTD Bách khoa 2022
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa đường thẳng $B'C$ và mặt phẳng \(\left( {BDD'B'} \right)\) bằng
Trả lời bởi giáo viên
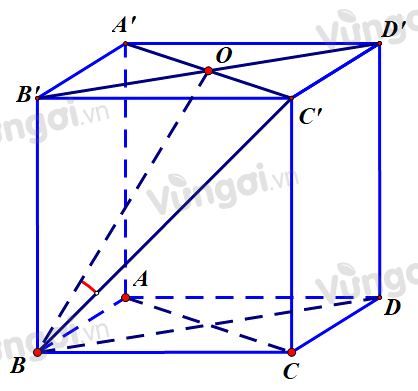
Gọi O là tâm của A’B’C’D’.
Ta có: \(C'O \bot \left( {BCC'B'} \right)\)
\( \Rightarrow O\) là hình chiếu của $C’$ lên \(\left( {BDD'B'} \right)\)
\( \Rightarrow BO\) là hình chiếu của $BC’$ lên \(\left( {BDD'B'} \right)\)
\( \Rightarrow \widehat {\left( {BC';\left( {BDD'B'} \right)} \right)} = \widehat {C'BO}\)
Giả sử cạnh của hình lập phương là 1.
Ta có:
\(\begin{array}{l}BC' = A'C' = \sqrt 2 \Rightarrow OC' = \dfrac{{\sqrt 2 }}{2}\\ \Rightarrow \sin \widehat {C'BO} = \dfrac{{OC'}}{{BC'}} = \dfrac{1}{2}\\ \Rightarrow \widehat {C'BO} = {30^0}\end{array}\)
Hướng dẫn giải:
- Gọi $O$ là tâm của $A’B’C’D’$.
- Xác định góc gữa $BC’$ và \(\left( {BDD'B'} \right)\).
- Tính góc gữa $BC’$ và \(\left( {BDD'B'} \right)\).