Đề thi chính thức ĐGTD Bách khoa 2022
Trong không gian \(Ozyz\), cho hai điểm \(A\left( {2;1;0} \right)\) và \(B\left( {0;4;0} \right).\) Xét điểm S thay đổi luôn thuộc trục \(Oz\), gọi \(K\) là trung điểm của \(SB,H\) là hình chiếu vuông góc của \(O\) trên \(AK\). Biết rằng \(H\) luôn thuộc một đường tròn cố định, chu vi của đường tròn đó là
Trả lời bởi giáo viên
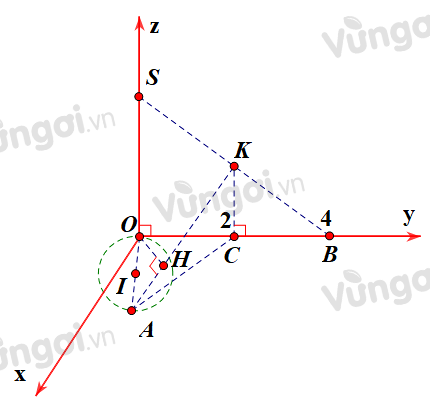
Gọi I là trung điểm của OA, C là trung điểm của OB=>\(C\left( {0;2;0} \right)\); \(I\left( {1;\dfrac{1}{2};0} \right)\)
=> CK//Oz=>(ACK)//Oz.
Ta có: \(OH \bot AK \Rightarrow H\) luôn thuộc mặt cầu tâm I đường kính OA.
Mặt khác H thuộc AK nên H thuộc mặt phẳng qua (AKC)
=> H luôn thuộc đường tròn giao tuyến của mặt phẳng (AKC) và mặt cầu (I)
Gọi r là bán kính đường tròn.
Khi đó \(r = \sqrt {O{I^2} - {{\left[ {d\left( {I;\left( {ACK} \right)} \right)} \right]}^2}} \)
Ta có: \(OI = \dfrac{{IA}}{2} = \dfrac{{\sqrt 5 }}{2}\)
\(\overrightarrow {AC} = \left( { - 2;1;0} \right)\)\(\overrightarrow n = \left[ {\overrightarrow {AC} ;\overrightarrow k } \right] = \left( { - 1; - 2;0} \right)\)
Mặt phẳng ACK:
\(\begin{array}{l}1.\left( {x - 2} \right) + 2.\left( {y - 1} \right) = 0 \Leftrightarrow x + 2y - 4 = 0\\ \Rightarrow d\left( {I;\left( {ACK} \right)} \right) = \dfrac{{\left| {1 + 1 - 4} \right|}}{{\sqrt 5 }} = \dfrac{2}{{\sqrt 5 }}\end{array}\)
\( \Rightarrow r = \dfrac{{3\sqrt 5 }}{{10}} \Rightarrow C = 2\pi r = \dfrac{{3\sqrt 5 \pi }}{5}\)
Hướng dẫn giải:
- Gọi I là trung điểm của OA, C là trung điểm của OB
- Gọi r là bán kính đường tròn.
- Xác định 1 mặt cầu và 1 mặt phẳng chứa H, từ đó xác định đường tròn luôn đi qua H.
- Sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng.
Câu hỏi khác
- Đề thi thử phần Toán ĐGTD Đại học Bách Khoa Hà Nội lần 1, có đáp án và lời giải chi tiết
- Đề thi thử phần Toán ĐGTD Đại học Bách Khoa Hà Nội lần 2, có đáp án và lời giải chi tiết
- Đề thi chính thức ĐGTD Bách khoa 2022 - mã 103 có đáp án và lời giải chi tiết
- Đề thi thử ĐGTD Bách khoa trường Yên Lạc - Lần 2 có đáp án và lời giải chi tiết
