Đề thi chính thức ĐGTD Bách khoa 2022
Cho một khối trụ tròn xoay và tam giác ABC vuông cân tại A, trong đó A, B nằm trên đường tròn đáy của khối trụ và C nằm trên đường tròn đáy còn lại. Biết \(AB = a\), mặt phẳng \(\left( {ABC} \right)\) tạo với mặt phẳng đáy của khối trụ một góc bằng \({45^o}\). Thể tích khối trụ đã cho bằng
Trả lời bởi giáo viên
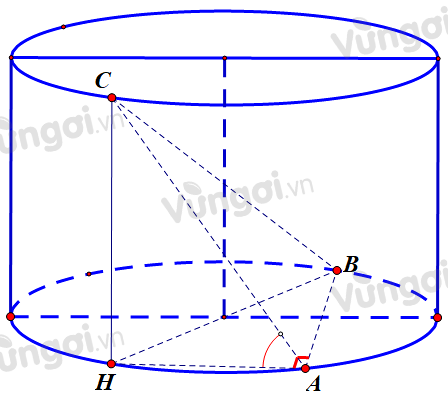
Vì ABC vuông cân tại A nên C thuộc mặt phẳng qua A và vuông góc với AB. Gọi H là giao điểm thứ 2 của mặt phẳng và đường tròn chứa A.
Mà C thuộc đường tròn đáy còn lại nên C là giao điểm của mặt phẳng trên và đường tròn đáy.
Khi đó ta có: \(\left( {CAH} \right) \bot AB \Rightarrow \widehat {\left( {\left( {ABC} \right),\left( {ABH} \right)} \right)} = \widehat {CAH}\)\( \Rightarrow \widehat {CAH} = {45^0}\)
\(\begin{array}{l}CA = AB = a \Rightarrow AH = CH = \dfrac{a}{{\sqrt 2 }}\\\left( {CAH} \right) \bot AB \Rightarrow AB \Rightarrow HA\\ \Rightarrow BH = \sqrt {A{B^2} + H{A^2}} = a\sqrt {\dfrac{3}{2}} \\ \Rightarrow {R_{day}} = \dfrac{1}{2}BH = \dfrac{{a\sqrt 6 }}{4}\end{array}\)
Thể tích hình trụ: \(V = \pi {R^2}h = \pi .\dfrac{{6{a^2}}}{{16}}.\dfrac{a}{{\sqrt 2 }} = \dfrac{{3\sqrt 2 {a^3}\pi }}{{16}}\)
Hướng dẫn giải:
- Xác định mặt phẳng qua A và vuông góc với AB, tìm điểm C.
- Gọi H là giao điểm thứ 2 của mặt phẳng và đường tròn chứa A.
- Tính CH và chứng minh BH là đường kính đường tròn đáy.
- Áp dụng công thức tính thể tích hình trụ.