Bạn Bách thả 1 quả bóng cao su từ độ cao 12m so với mặt đất. Mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng \(\dfrac{2}{3}\) độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng số quãng đường quả bóng đã di chuyển (từ lúc thả bóng cho tới khi quả bóng không nảy nữa) gần nhất với kết quả nào sau đây?
Trả lời bởi giáo viên
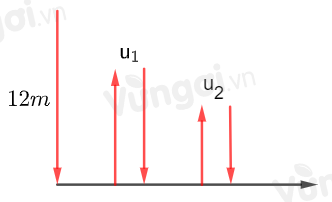
Ta coi độ cao nảy lên lần thứ nhất là \({u_1} \Rightarrow {u_1} = 12.\dfrac{2}{3} = 8\)
\( \Rightarrow {u_2} = \dfrac{2}{3}{u_1};{u_3} = \dfrac{2}{3}{u_2};...;{u_n} = \dfrac{2}{3}{u_{n - 1}};...\)
=> Đây là cấp số nhân lùi vô hạn với \({u_1} = 8;q = \dfrac{2}{3}\)
Khi đó tổng quãng đường quả bóng đã di chuyển là
\(S = 12 + 2{u_1} + 2{u_2} + 2{u_3} + ... + 2{u_n} + ...\)
$=12+2.(u_1+u_2+…)$$=12+2.\dfrac{u_1}{1-q}$
\( = 12 + 2.\dfrac{8}{{1 - \dfrac{2}{3}}} = 60\)
Hướng dẫn giải:
- Xác định cấp số nhân.
- Sử dụng công thức tính tổng n số hạng đầu của cấp số nhân lùi vô hạn.