Trong không gian với hệ trục Oxyz, cho \(d:\dfrac{{x - 4{m^2}}}{2} = \dfrac{{y + 2m}}{{ - 2}} = \dfrac{{z + 2}}{1}\) và \(A\left( { - 1;2;1} \right),B\left( {1; - 2;0} \right)\). Gọi C, D lần lượt là hình chiếu vuông góc của A, B lên d. biết khối tứ diện ABCD có thể tích nhỏ nhất. khẳng định nào dưới đây đúng?

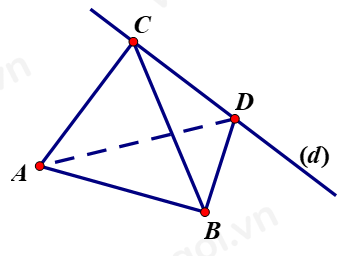
Mặt phẳng (P) qua A và vuông góc với đường thẳng (d) là:

\(2\left( {x + 1} \right) - 2\left( {y - 2} \right) + \left( {z - 1} \right) = 0\)\( \Leftrightarrow 2x - 2y + z + 5 = 0\)

Mặt phẳng (Q) qua B và vuông góc với (d) là:

\(2x - 2y + z - 6 = 0\)

Khi đó C là giao điểm của (P) và d, D là giao điểm của (Q) và d

\(CD = d\left( {\left( P \right),\left( Q \right)} \right) = \dfrac{{11}}{3}\)

Đường thẳng d qua \(E\left( {4{m^2}; - 2m; - 2} \right)\) và nhận vecto chỉ phương \(\overrightarrow u \left( {2; - 2;1} \right)\)

Đường thẳng AB qua \(A\left( { - 1;2;1} \right)\) và nhận vecto chỉ phương \(\overrightarrow {AB}  = \left( {2; - 4; - 1} \right)\)

Gọi \(\alpha \) là góc giữa 2 đường thẳng (d) và (AB), khi đó \(\sin \alpha \) là hằng số.

Khoảng cách giữa (d) và (AB) là: \(d\left( {d;AB} \right) = \dfrac{{\left| {\left[ {\overrightarrow u ;\overrightarrow {AB} } \right].\overrightarrow {AI} } \right|}}{{\left| {\left[ {\overrightarrow u ;\overrightarrow {AB} } \right]} \right|}} = \dfrac{{24{m^2} - 8m + 10}}{{2\sqrt {17} }}\) min tại \(m = \dfrac{1}{6}\)

\({V_{ABCD}} = \dfrac{1}{6}d\left( {d;AB} \right).CD.AB.\sin \alpha \) đạt giá trị nhỏ nhất

\( \Leftrightarrow d\left( {d;AB} \right)\min  \Leftrightarrow m = \dfrac{1}{6} \Rightarrow m \in \left( {0;\dfrac{1}{4}} \right)\)