Câu hỏi:
3 năm trước
Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = 2a,SA = a\sqrt 5 \). Khoảng cách từ đường thẳng \(AB\) đến \((SCD)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: b
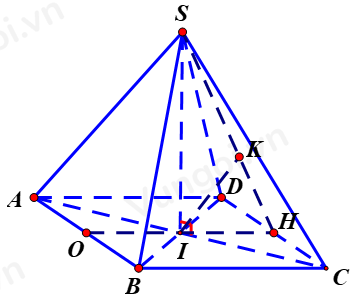
Gọi \({\rm{I }} = AC \cap BD.\)
\(AB = 2a \Rightarrow AI = a\sqrt 2 \)
\( \Rightarrow SI = \sqrt {S{A^2} - A{I^2}} = \sqrt {{{(a\sqrt S )}^2} - {{(a\sqrt 2 )}^2}} = a\sqrt 3 \)
Do \(AB//CD \Rightarrow d(AB;SCD) = d(;SCD) = 2d(;SCD)\)
Kẻ \(IH \bot CD;IK \bot SH = d(A;SCD) = IK\)
\(\dfrac{1}{{I{K^2}}} = \dfrac{1}{{S{I^2}}} + \dfrac{1}{{I{H^2}}} \Rightarrow IN = \dfrac{{a\sqrt 3 }}{2}\)
\( \Rightarrow d(AB;SCD) = a\sqrt 3 \)
Hướng dẫn giải:
- Gọi \({\rm{I }} = AC \cap BD.\)
- Kẻ \(IH \bot CD;IK \bot SH = d(A;SCD) = IK\)
- Tính IN