Một chiếc xe cứu hộ xuất phát từ góc của một hồ nước hình chữ nhật có các cạnh dài \(1600\;{\rm{m}}\) và rộng \(600\;{\rm{m}}\). Xe vừa có thể đi trên bờ hồ và đi trên mặt nước với vận tốc tương ứng là \(20\;{\rm{m}}/{\rm{s}}\) và \(12\;{\rm{m}}/{\rm{s}}\). Tính thời gian xe đi nhanh nhất đến tâm của hồ.

Đáp án:
s
Trả lời bởi giáo viên
Đáp án:
s
TH1: Đặt \(AM = x{\rm{. }}\)
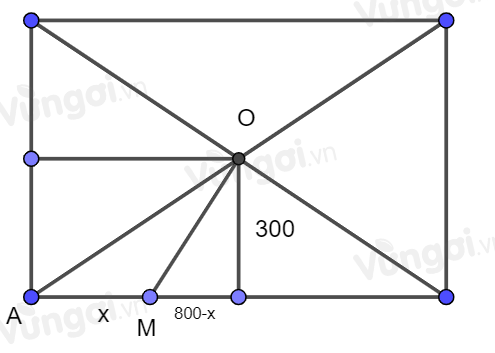
Xe cứu hộ đi theo hướng \({\rm{AMO }}\)
Thời gian đi của xe là:
\(t\left( x \right) = \dfrac{{AM}}{{20}} + \dfrac{{MO}}{{12}}\)
\( = \dfrac{x}{{20}} + \dfrac{{\sqrt {{{300}^2} + {{(800 - x)}^2}} }}{{{1^2}}}\)
\( = \dfrac{x}{{20}} + \dfrac{{\sqrt {{x^2} - 1600x + 730000} }}{{12}}\)
Ta có:
\({t^\prime }(x) = \dfrac{1}{{20}} + \dfrac{1}{{12}} \cdot \dfrac{{2x - 1600}}{{2\sqrt {{x^2} - 1600x + 730000} }} = 0\)
\( \Rightarrow x = 575\)
\( \Rightarrow {t_{\min }} = t(525) = 60{\rm{ (s)}}\)
TH2: Đặt \(AN = x\)
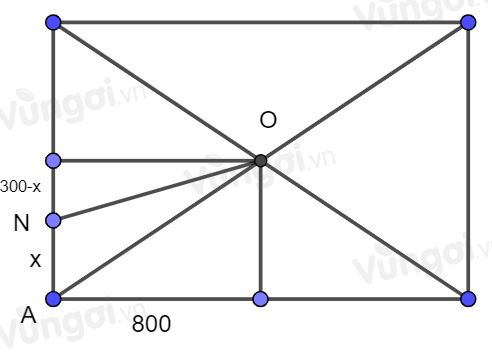
Xe cứu hộ đi theo hướng ANO.
Thời gian đi của xe là:
\(t\left( x \right) = \dfrac{{AN}}{{20}} + \dfrac{{NO}}{{12}}\)
\( = \dfrac{x}{{20}} + \dfrac{{\sqrt {{{800}^2} + {{(300 - 2)}^2}} }}{{12}}\)
\({t^\prime }(x) = 0 \Leftrightarrow x = - 300{\rm{ (s)}}\)(loại)
Vậy thời gian nhanh nhất xe đi đến tâm là 60(s).
Hướng dẫn giải:
Xét 2 trường hợp
TH1: Đặt \(AM = x{\rm{. }}\)Xe cứu hộ đi theo hướng \({\rm{AMO }}\)
TH2: Đặt \(AN = x\). Xe cứu hộ đi theo hướng ANO.
- Lập hàm số t(x) biểu diễn thời gian đi của xe
- Giải t’(x)=0 và tìm x